题目内容
一杂技运动员骑摩托车沿一竖直圆轨道做特技表演，如图K22－10所示．若车运动的速率恒为20 m/s，人与车质量之和为200 kg，车所受阻力与轨道间的弹力成正比(比例系数k＝0.1)．车通过最低点A时发动机的功率为12 kW，求车通过最高点B 时发动机的功率为多少？(取g＝10 m/s2)
图K22－10
4 kW
[解析] 摩托车经最低点A时，由牛顿第二定律
FN1－mg＝m
轨道对车的支持力为FN1＝mg＋m
车在最高点B时，由牛顿第二定律知
mg＋FN2＝m
轨道对车的支持力为FN2＝m－mg
车在最低点A时，发动机的功率P1＝kFN1v
车在最高点B时，发动机的功率为P2＝kFN2v
联立以上各式解得P2＝4 kW
练习册系列答案
高中必刷题系列答案
相关题目
一杂技运动员骑摩托车沿一竖直圆形轨道做特技表演，若车运动的速率恒为20m/s，人与车的总质量为200kg，轮胎与轨道间的摩擦力大小总与它们间的正压力成正比，且比例系数为μ=0.1，车通过最底点B时发动机功率为12kw．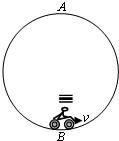
如图所示，一杂技运动员骑摩托车沿着一竖直圆轨道做特技表演，若摩托车运动的速率恒为v=20m/s，人和车的总质量为m=200m/s，摩托车受到的阻力是摩托车对轨道压力的k倍，且k=0.1．摩托车通过最高点A时发动机的功率为零，（摩托车车身的长不计，g=10m/s2）求：