题目内容
11.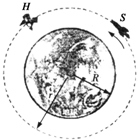 一组宇航员乘坐太空穿梭机S,去修理位于离地球表面h=6.0×105m的圆形轨道上的太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,望远镜在穿梭机前方数千米处,如图所示.已知地球半径为R=6.4×106m,地球表面重力加速度为g=9.8m/s2,第一宇宙速度为v=7.9km/s.
一组宇航员乘坐太空穿梭机S,去修理位于离地球表面h=6.0×105m的圆形轨道上的太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,望远镜在穿梭机前方数千米处,如图所示.已知地球半径为R=6.4×106m,地球表面重力加速度为g=9.8m/s2,第一宇宙速度为v=7.9km/s.(1)穿梭机所在轨道上的向心加速度g′为多少?
(2)计算穿梭机在轨道上的速率v′;
(3)穿梭机需先进入半径较小的轨道,才有较大的角速度追上望远镜.试判断穿梭机要进入较低轨道时应增加还是减小其原有速率,试说明理由.
分析 卫星在原有轨道上加速做离心运动,轨道半径增大,在原有轨道上减速做向心运动,轨道半径减小.
根据万有引力提供向心力$G\frac{Mm}{{(R+h)}^{2}}=mg′$,以及地球表面上的物体受到的重力等于万有引力$G\frac{Mm}{{R}^{2}}=mg$,化简得到加速度的表达式,代入数据计算即可
解答 解:(1)由mg=G$\frac{Mm}{{R}^{2}}$,得地球表面的重力加速度为g=$\frac{GM}{{R}^{2}}$,
同理穿梭机所在轨道上的向心加速度为g′=$\frac{GM}{r2}$
联立以上二式并代入数据解得:g′=8.2m/s2
(2)由G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,可得第一宇宙速度为:v=$\sqrt{\frac{GM}{R}}$
同理穿梭机在轨道上的速率为:v′=$\sqrt{\frac{GM}{r}}$
代入数据解得:v′=7.6km/s
(3)应减速.由G$\frac{Mm}{{r}^{2}}$=m$\frac{v{′}^{2}}{r}$知穿梭机要进入较低轨道,必须有万有引力大于穿梭机做圆周运动所需的向心力,故当v′减小时,m$\frac{v{′}^{2}}{r}$才减小,则G$\frac{Mm}{{r}^{2}}$>m$\frac{v{′}^{2}}{r}$.
答:(1)穿梭机所在轨道上的向心加速度g′为8.2m/s2;
(2)计算穿梭机在轨道上的速率v′为7.6km/s;
(3)应减速,穿梭机要进入较低轨道,必须有万有引力大于穿梭机做圆周运动所需的向心力.
点评 本题关键抓住万有引力提供向心力和重力等于万有引力,列式求解出加速度的表达式,代入数据进行计算.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.一矩形线圈在匀强磁场中匀速转动时,产生的交变电动势的图象如图所示,则( )


| A. | 交变电流的频率是4πHz | B. | 当t=0时,线圈平面与磁感线垂直 | ||
| C. | 当t=πs时,e有最大值 | D. | 交流电的周期是πs |
2. 如图所示,滑块以速率v1沿斜面由底端向上滑行,至某一位置后返回,回到出发点时的速率变为v2,且v2<v1,则下列说法中正确的是( )
如图所示,滑块以速率v1沿斜面由底端向上滑行,至某一位置后返回,回到出发点时的速率变为v2,且v2<v1,则下列说法中正确的是( )
 如图所示,滑块以速率v1沿斜面由底端向上滑行,至某一位置后返回,回到出发点时的速率变为v2,且v2<v1,则下列说法中正确的是( )
如图所示,滑块以速率v1沿斜面由底端向上滑行,至某一位置后返回,回到出发点时的速率变为v2,且v2<v1,则下列说法中正确的是( )| A. | 全过程中重力做功为零 | |
| B. | 在上滑和下滑两过程中,摩擦力做功不等 | |
| C. | 在上滑过程中摩擦力的平均功率大于下滑过程中摩擦力的平均功率 | |
| D. | 全过程中摩擦力不做功 |
6. 如图所示,木板放在光滑地面上,将一滑块m用恒力F由木块一端拉至另一端,木板分固定和不固定两种情况,力F做功分别为W1和W2,产生的热量分别是Q1和Q2则( )
如图所示,木板放在光滑地面上,将一滑块m用恒力F由木块一端拉至另一端,木板分固定和不固定两种情况,力F做功分别为W1和W2,产生的热量分别是Q1和Q2则( )
 如图所示,木板放在光滑地面上,将一滑块m用恒力F由木块一端拉至另一端,木板分固定和不固定两种情况,力F做功分别为W1和W2,产生的热量分别是Q1和Q2则( )
如图所示,木板放在光滑地面上,将一滑块m用恒力F由木块一端拉至另一端,木板分固定和不固定两种情况,力F做功分别为W1和W2,产生的热量分别是Q1和Q2则( )| A. | W1<W2 | B. | W1=W2 | C. | Q1=Q2 | D. | Q1<Q2 |
3.在探究平抛运动的规律时,可以选用下图所示的各种装置图,以下说法正确的是( )


| A. | 选用装置1可以研究平抛物体的水平分运动 | |
| B. | 选用装置2时,要获得稳定的细水柱所显示的平抛轨迹,竖直管上端A一定要低于水面 | |
| C. | 选用装置3时,要获得钢球的平抛轨迹,每次不一定要从斜槽上同一位置由静止释放钢球 | |
| D. | 除上述装置外,也能用数码照相机拍摄钢球做平抛运动的每秒十几帧至几十帧的照片,获得平抛轨迹 |
20.如图所示,一只小鸟沿着较粗的均匀树枝从右向左缓慢爬行,在小鸟从A运动到B的过程中( )


| A. | 树枝对小鸟的合作用力先减小后增大 | |
| B. | 树枝对小鸟的摩擦力先减小后增大 | |
| C. | 树枝对小鸟的弹力先减小后增大 | |
| D. | 树枝对小鸟的弹力保持不变 |
 如图所示,光滑的倾斜轨道与半径为R的圆形轨道相连接,质量为m的小球在倾斜轨道上由静止释放,要使小球恰能通过圆形轨道的最高点,求:
如图所示,光滑的倾斜轨道与半径为R的圆形轨道相连接,质量为m的小球在倾斜轨道上由静止释放,要使小球恰能通过圆形轨道的最高点,求: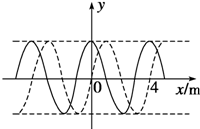 如图实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.求:
如图实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.求: 在用两面平行的玻璃砖测定玻璃折射率的实验中,
在用两面平行的玻璃砖测定玻璃折射率的实验中,