题目内容
2.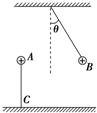 如图所示,若固定的带正电小球A的电荷量为Q,一个挂在不远处绝缘细线下端的带正电的小球B,静止在图示位置,B球的质量为m,带电荷量为q,θ=30°,A和B在同一条水平线上,整个装置处于真空中,此时两球球心相距L.求:
如图所示,若固定的带正电小球A的电荷量为Q,一个挂在不远处绝缘细线下端的带正电的小球B,静止在图示位置,B球的质量为m,带电荷量为q,θ=30°,A和B在同一条水平线上,整个装置处于真空中,此时两球球心相距L.求:(1)小球B受到的电场力大小
(2)场源A产生的电场在B处的场强.
分析 (1)B小球在A球电场中处于平衡,利用平衡列方程求解即可求得电场力.
(2)根据场强的定义式可求得电场强度.
解答  解:(1)根据题意,A、B两球都受力平衡,对B球进行受力分析,
解:(1)根据题意,A、B两球都受力平衡,对B球进行受力分析,
根据平衡可知:F=mgtanθ=$\frac{\sqrt{3}mg}{3}$
(2)根据场强公式E=$\frac{F}{q}$得:
E=$\frac{\sqrt{3}mg}{3q}$,场强方向由A指向B
答:(1)小球B受到的电场力大小为$\frac{\sqrt{3}mg}{3}$
(2)场源A产生的电场在B处的场强为$\frac{\sqrt{3}mg}{3q}$.方向由A指向B.
点评 本题考查灵活利用平衡态列方程是解题的关键,注意场强的定义式,注意明确电场力的性质,然后即可将电场力作为普通力和其他力一起受力分析,根据平衡条件即可求解.

练习册系列答案
相关题目
4.在平直道路上,甲汽车以速度v行驶,当甲车司机发现前方距离为d处的乙汽车时,立即以大小为a1的加速度匀减速行驶,与此同时,乙车司机也发现了甲,立即从静止开始以大小为a2的加速度沿甲运动的方向匀加速运动.则( )
| A. | 若$v>2\sqrt{({{a_1}+{a_2}})d}$,则两车一定不会相撞 | |
| B. | 若$v<2\sqrt{({{a_1}+{a_2}})d}$,则两车一定不会相撞 | |
| C. | 若$v>\sqrt{2({{a_1}+{a_2}})d}$,则两车一定不会相撞 | |
| D. | 若$v<\sqrt{2({{a_1}+{a_2}})d}$,则两车一定不会相撞 |
17. 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固体电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固体电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固体电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固体电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )| A. | 电阻R1消耗的热功率为$\frac{Fv}{3}$ | |
| B. | 电阻R2消耗的热功率为$\frac{Fv}{6}$ | |
| C. | 整个装置因摩擦而消耗的热功率为μmgvcosθ | |
| D. | 整个装置消耗的电功率为Fv |
11. 在空间某一静电场中选取某一方向建立坐标x轴,电势φ在x轴上分布如图所示,x轴上两点B、C点电场强度分别是EB、EC,下列说法中正确的有( )
在空间某一静电场中选取某一方向建立坐标x轴,电势φ在x轴上分布如图所示,x轴上两点B、C点电场强度分别是EB、EC,下列说法中正确的有( )
 在空间某一静电场中选取某一方向建立坐标x轴,电势φ在x轴上分布如图所示,x轴上两点B、C点电场强度分别是EB、EC,下列说法中正确的有( )
在空间某一静电场中选取某一方向建立坐标x轴,电势φ在x轴上分布如图所示,x轴上两点B、C点电场强度分别是EB、EC,下列说法中正确的有( )| A. | EB的大小一定大于EC的大小 | |
| B. | EC的方向一定沿x轴正方向 | |
| C. | 将一负电荷沿x轴从B移到C的过程中,电场力先做正功,后做负功 | |
| D. | 将一负电荷沿x轴从B移到C的过程中,电荷动能先增加后减小 |
 在磁感应强度为1T的匀强磁场中,有一边长为20cm的10匝正方形线圈,线圈的总电阻为1Ω,线圈外接一阻值为9Ω的电阻R,若以某一边长为轴在磁场中10rad/s的角速度匀速转动,求:
在磁感应强度为1T的匀强磁场中,有一边长为20cm的10匝正方形线圈,线圈的总电阻为1Ω,线圈外接一阻值为9Ω的电阻R,若以某一边长为轴在磁场中10rad/s的角速度匀速转动,求: 如图所示,两足够长的平行光滑金属导轨MN、PQ相距为L,导轨平面与水平面的夹角为α,匀强磁场分布在整个导轨所在区城,磁感应强度为B、方向垂直于导轨平面向上,质量为m、长为L的金属杆垂直于MN,PQ放置在导轨上,且始终与导轨接触良好.两导轨的上端通过导线连接由定值电阻和电容器组成的电路,电容器的电容为C.现闭合开关S并将金属杆从ab位置由静止释放,已知杆向下运动距离为x到达cd位置的过程中,通过杆的电荷量为q1,通过定值电阻的电荷量为q2,且已知杆在到达cd前已达到最大速度.不计导轨、金属杆及导线的电阻,重力加速度为g.
如图所示,两足够长的平行光滑金属导轨MN、PQ相距为L,导轨平面与水平面的夹角为α,匀强磁场分布在整个导轨所在区城,磁感应强度为B、方向垂直于导轨平面向上,质量为m、长为L的金属杆垂直于MN,PQ放置在导轨上,且始终与导轨接触良好.两导轨的上端通过导线连接由定值电阻和电容器组成的电路,电容器的电容为C.现闭合开关S并将金属杆从ab位置由静止释放,已知杆向下运动距离为x到达cd位置的过程中,通过杆的电荷量为q1,通过定值电阻的电荷量为q2,且已知杆在到达cd前已达到最大速度.不计导轨、金属杆及导线的电阻,重力加速度为g. 如图所示,质量为m,带+q电量的滑块,沿绝缘斜面匀速下滑,当滑至竖直向下的匀强电场区时,滑块将做匀速运动.
如图所示,质量为m,带+q电量的滑块,沿绝缘斜面匀速下滑,当滑至竖直向下的匀强电场区时,滑块将做匀速运动. 如图所示,两带电平行板竖直放置,开始时两极板间电压为U,相距为d,两极板间形成匀强电场.有一带电粒子,质量为m(重力不计)、所带电荷量为+q,从两极板下端连线的中点P以竖直速度v0射入匀强电场中,带电粒子落在A极板的M点上.
如图所示,两带电平行板竖直放置,开始时两极板间电压为U,相距为d,两极板间形成匀强电场.有一带电粒子,质量为m(重力不计)、所带电荷量为+q,从两极板下端连线的中点P以竖直速度v0射入匀强电场中,带电粒子落在A极板的M点上. 带电量为q,质量为m的原子核由静止开始经电压为U1的电场加速后进入一个平行板电容器,进入时速度和电容器中的场强方向垂直.已知:电容器的极板长为L,极板间距为d,两极板的电压为U2,重力不计,求:
带电量为q,质量为m的原子核由静止开始经电压为U1的电场加速后进入一个平行板电容器,进入时速度和电容器中的场强方向垂直.已知:电容器的极板长为L,极板间距为d,两极板的电压为U2,重力不计,求: