题目内容
长L=0.5m、质量可以忽略的杆，一端固定于O点，另一端连有质量m=2Kg的小球，它绕O点做竖直平面内的圆周运动，当通过最高点时，如图所示，求下列情况下小球所受到的力（计算出大小，并说明是拉力还是支持力）．（1）当v=1m/s时，大小为 N，是 力；
（2）当v=4m/s时，大小为 ，是 力．
【答案】分析：由于物体做圆周运动需要向心力，所以对小球在最高点受力分析，仅受重力与杆子在竖直方向的做用力，二力的合力提供向心力列牛顿第二定律解决．
解答：
解：对小球受力分析，假设杆子对小球的作用力方向竖直向上大小为F：
根据牛顿第二定律：mg-F=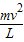
（1）当v=1m/s时，解得：F=mg-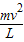
=16N
故杆子对小球的作用力大小为16N，方向向上．
根据牛顿第三定律小球对杆子的作用力为向下的压力，大小为16N．
（2）当v=4m/s时，解得：F=mg-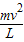
=-44N，负号表示力F的方向与题目假设的方向相反，
故杆子对小球的作用力大小为44N，方向向下．
根据牛顿第三定律小球对杆子的作用力为向上的拉力，大小为44N．
故答案为：16，压；44，拉
点评：注意当无法确定力的方向时，可以先假设到某一方向上，如果解出的结果为正值，说明力就在假设的方向上，如果解出的结果为负值，说明力的方向与假设的方向相反．
解答：
解：对小球受力分析，假设杆子对小球的作用力方向竖直向上大小为F：根据牛顿第二定律：mg-F=
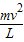
（1）当v=1m/s时，解得：F=mg-
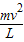=16N故杆子对小球的作用力大小为16N，方向向上．
根据牛顿第三定律小球对杆子的作用力为向下的压力，大小为16N．
（2）当v=4m/s时，解得：F=mg-
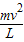=-44N，负号表示力F的方向与题目假设的方向相反，故杆子对小球的作用力大小为44N，方向向下．
根据牛顿第三定律小球对杆子的作用力为向上的拉力，大小为44N．
故答案为：16，压；44，拉
点评：注意当无法确定力的方向时，可以先假设到某一方向上，如果解出的结果为正值，说明力就在假设的方向上，如果解出的结果为负值，说明力的方向与假设的方向相反．
练习册系列答案
相关题目
如图所示，水平面上有两根相距0.5m 的足够长的光滑平行金属导轨MN 和PQ，它们的电阻可忽略不计，在M和P之间接有阻值为R=3.0Ω 的定值电阻，导体棒ab长l=0.5m，质量m=1kg，其电阻为r=1.0Ω，与导轨接触良好．整个装置处于方向竖直向上的匀强磁场中，磁感应强度B=0.4T．现使ab 以v0=10m/s 的速度向右做匀速运动．
如图所示，水平面上有两根相距0.5m的足够长的固定平行金属导轨MN和PQ，它们的电阻可忽略不计，在M和P之间接有阻值R=3.0Ω的定值电阻．导体棒ab长l=0.5m，质量m=0.1kg，其电阻r=1.0Ω，与导轨接触良好，它们之间的动摩擦因数μ=0.1．整个装置处于方向竖直向上的匀强磁场中，磁感应强度B=0.4T．现在恒力F的作用下使导体棒ab以v=10m/s的速度向右做匀速运动．求：
如图所示，Ⅰ、Ⅱ区域是宽度均为L=0.5m的匀强磁场，磁感应强度大小B=1T，方向相反．一边长L=0.5m、质量m=0.1kg、电阻R=0.5Ω的正方形金属线框，在外力作用下，以初速度v0=10m/s匀速穿过磁场区域．
如图长l=0.5m，质量可忽略的杆，其下端固定于O点，上端连有质量m=2kg的小球，它绕O点作圆周运动，当通过最高点时，求下列情况下，当v=1m/s，杆受到的力大小为
如图所示，正方形线框abcd放在光滑绝缘的水平面上，其边长L=0.5m、质量m=0.5kg、电阻R=0.5Ω，M、N分别为线框ad、bc边的中点．图示两个虚线区域内分别有竖直向下和向上的匀强磁场，磁感应强度均为B=1T，PQ为其分界线．线框从图示位置以速度