题目内容
6.小球A和B的质量分别为mA=2kg和mB=1kg,在离地面高h1=5m处从同一位置将A和B先后由静止释放.小球A与水平地面碰撞后向上弹起,小球A弹起的最大高度为h2=3.2m,当小球A到达最高点时正好与下落的小球B发生正碰.设小球A和B碰撞是弹性碰撞且碰撞时间极短.重力加速度g=10m/s2(1)求小球A、B碰撞后B上升的最大高度;
(2)若已知小球A与地面作用的时间t=0.1s,求地面对小球A的平均作用力大小.
分析 由于AB是从同一高度释放的,并且碰撞过程中没有能量的损失,根据机械能守恒可以求得碰撞时的速度的大小,再根据A、B碰撞过程中动量守恒,可以求得碰后的速度大小,进而求可以得A、B碰撞后B上升的最大高度,根据动量定理求解.
解答 解:(1)碰前小球B的速度为:vB=$\sqrt{2g({h}_{1}-{h}_{2})}$=6m/s
设竖直向下的方向为正方向,由动量守恒得:
mBvB=mAvA′+mBvB′
即1×6=2×vA′+1×vB′
碰撞前后机械能守恒,有:$\frac{1}{2}{{m}_{B}v}_{B}^{2}$=$\frac{1}{2}{m}_{A}{v}_{A}{′}^{2}$+$\frac{1}{2}$mB${v′}_{B}^{2}$
$\frac{1}{2}$×1×62=$\frac{1}{2}$×2 ${v}_{A}^{′2}$+$\frac{1}{2}×$1×${v}_{B}^{′2}$
解得碰后小球B的速度为:vB′=-2m/s
碰后B上升的最大高度为:h=$\frac{{{v′}_{B}}^{2}}{2g}$=0.2m
(2)小球A落地前的速度为:v0=$\sqrt{2g{h}_{1}}$=10m/s
小球A弹起后的速度为:vt=$\sqrt{2g{h}_{2}}$=8m/s
Ft-mgt=mAvt-mA(-v0)
解得:F=380N
答(1)小球A、B碰撞后B上升的最大高度0.2m;
(2)地面对小球A的平均作用力大小
点评 本题考查的是机械能守恒的应用,同时在碰撞的过程中物体的动量守恒,在利用机械能守恒和动量守恒的时候一定注意各自的使用条件,将二者结合起来应用即可求得本题

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案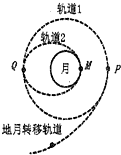 探月工程中,“嫦娥三号”探测器的发射可以简化如下:卫星由地面发射后,进入地月转移轨道,经过P点时变轨进入距离月球表面100公里圆形轨道1,在轨道1上经过Q点时月球车将在M点着陆月球表面,不正确的是( )
探月工程中,“嫦娥三号”探测器的发射可以简化如下:卫星由地面发射后,进入地月转移轨道,经过P点时变轨进入距离月球表面100公里圆形轨道1,在轨道1上经过Q点时月球车将在M点着陆月球表面,不正确的是( )| A. | “嫦娥三号”在轨道1上的速度比月球的第一宇宙速度小 | |
| B. | “嫦娥三号”在地月转移轨道上经过P点的速度比在轨道1上经过P点时大 | |
| C. | “嫦娥三号”在轨道1上运动周期比在轨道2上小 | |
| D. | “嫦娥三号”在轨道1上经过Q点时的加速度小于在轨道2上经过Q点时的加速度 |
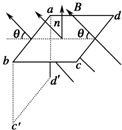 如图所示,面积为S的矩形导线框abcd,处在磁感应强度为B的匀强磁场中,磁场方向与线框平面成θ角.当线框从图示位置以ab为轴顺时针匀速转90°过程中,下列判断正确的是( )
如图所示,面积为S的矩形导线框abcd,处在磁感应强度为B的匀强磁场中,磁场方向与线框平面成θ角.当线框从图示位置以ab为轴顺时针匀速转90°过程中,下列判断正确的是( )| A. | 线框中电流先减小后增大 | |
| B. | 线框中电流先增大后减小 | |
| C. | 线框中电流方向一直为a→b→c→d→a | |
| D. | 线框中电流方向先为a→b→c→d→a,再为a→d→c→b→a |

| A. | 图象甲表明少量光子往往表现出粒子性,图象丙表明大量光子往往表现出波动性 | |
| B. | 图象丙中出现了明暗相间的干涉条纹,其中暗条纹处是光子到达不了的地方 | |
| C. | 光子的波动性是光子间相互作用形成的 | |
| D. | 该实验表明光是一种概率波 |
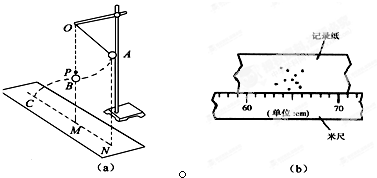
 如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某物体(可视为质点)从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面上的A、B两处.各处材质相同,忽略空气阻力,则( )
如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某物体(可视为质点)从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面上的A、B两处.各处材质相同,忽略空气阻力,则( )| A. | 此物体在曲面PC和斜面PD上克服摩擦力做功一定相等 | |
| B. | 此物体沿PCA和沿PDB运动克服摩擦力做功一定相等 | |
| C. | 距离OA一定等于OB | |
| D. | 距离OA一定小于OB |
| A. | 电视机不用时切断电源 | B. | 离开教室时随手关灯 | ||
| C. | 夏天用空调时,把温度调得很低 | D. | 尽量少开启电冰箱门 |
 如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B=0.5T,圆台母线与竖直方向的夹角为θ=37°,一个质量为m=0.8kg、周长为L=3m的匀质金属环位于圆台底部.给圆环通以恒定的电流I=8A后,圆环由静止向上做匀加速直线运动,经过时间t=2s后撤去该恒定电流并保持圆环闭合,圆环全程上升的最大高度为H.重力加速度为g=10m/s2,磁场的范围足够大.在圆环向上运动的过程中,下列说法正确的是(已知:sin37°=0.6,cos37°=0.8)( )
如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B=0.5T,圆台母线与竖直方向的夹角为θ=37°,一个质量为m=0.8kg、周长为L=3m的匀质金属环位于圆台底部.给圆环通以恒定的电流I=8A后,圆环由静止向上做匀加速直线运动,经过时间t=2s后撤去该恒定电流并保持圆环闭合,圆环全程上升的最大高度为H.重力加速度为g=10m/s2,磁场的范围足够大.在圆环向上运动的过程中,下列说法正确的是(已知:sin37°=0.6,cos37°=0.8)( )| A. | 圆环的最大速度为10m/s | B. | 圆环产生的最大电动势为6V | ||
| C. | 圆环上升过程中安培力做功32J | D. | 圆环先有收缩后有扩张的趋势 |
 质量m=4Kg的物体静止在水平长木板上,如图甲所示,则:
质量m=4Kg的物体静止在水平长木板上,如图甲所示,则: