题目内容
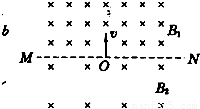
如图所示,以MN为界的两匀强磁场,磁感应强度B1=2B2,方向垂直纸面向里,现有一质量为m、带电量为q的正粒子,从O点沿图示方向进入B1中.(1)试画出此粒子的运动轨迹
(2)求经过多长时间粒子重新回到O点?
【答案】分析:(1)粒子在两种磁场中只受洛伦兹力,做匀速圆周运动,根据牛顿第二定律可知半径之比为1:2,根据左手定则,分析粒子旋转方向,画出轨迹.
(2)根据轨迹,确定时间与周期的关系,求出粒子重新回到O点的时间.
解答:解:(1)设粒子在磁场B1和B2中圆周运动的半径分别为r1、r2.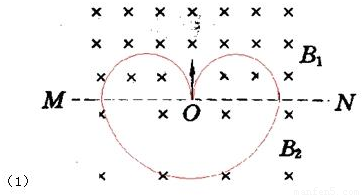
则r1=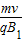 ,r2=
,r2=
由题B1=2B2,得r1:r2=1:2
根据左手定则判断可知,粒子在磁场B1中沿逆时针方向旋转,在磁场B2中沿顺时针方向旋转.则轨迹如图.
(2)粒子在磁场B1中运动时间t1=T1=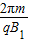
粒子在磁场B2中运动时间t2= T2=
T2=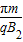
则t=t1+t2=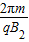
答:(1)粒子的运动轨迹如图.
(2)经过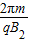 时间粒子重新回到O点.
时间粒子重新回到O点.
点评:本题重点考查作图能力.带电粒子在磁场中运动问题,画轨迹是解决这类问题的关键.
(2)根据轨迹,确定时间与周期的关系,求出粒子重新回到O点的时间.
解答:解:(1)设粒子在磁场B1和B2中圆周运动的半径分别为r1、r2.

则r1=
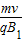 ,r2=
,r2=
由题B1=2B2,得r1:r2=1:2
根据左手定则判断可知,粒子在磁场B1中沿逆时针方向旋转,在磁场B2中沿顺时针方向旋转.则轨迹如图.
(2)粒子在磁场B1中运动时间t1=T1=
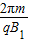
粒子在磁场B2中运动时间t2=
 T2=
T2=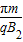
则t=t1+t2=
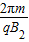
答:(1)粒子的运动轨迹如图.
(2)经过
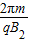 时间粒子重新回到O点.
时间粒子重新回到O点.点评:本题重点考查作图能力.带电粒子在磁场中运动问题,画轨迹是解决这类问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
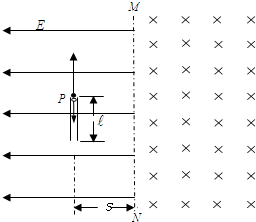 (2011?广安二模)我国科学家在对放射性元素的研究中,进行了如下实验:如图所示,以MN为界,左、右两边分别是电场强度为E的匀强电场和磁感应强度为B的匀强磁场,且两场区域足够大.在距离界线为S处平行于MN固定一内壁光滑的瓷管PQ,开始时一个放射性元素的原子核处在管口P处,某时刻该原子核平行于界线的方向放出一质量为m、带电量-e的电子,发现电子在分界线处速度方向与界线成60°角进入右边磁场,反冲核在管内做匀速直线运动,当到达管另一端Q点时,刚好俘获了这个电子而静止.求:
(2011?广安二模)我国科学家在对放射性元素的研究中,进行了如下实验:如图所示,以MN为界,左、右两边分别是电场强度为E的匀强电场和磁感应强度为B的匀强磁场,且两场区域足够大.在距离界线为S处平行于MN固定一内壁光滑的瓷管PQ,开始时一个放射性元素的原子核处在管口P处,某时刻该原子核平行于界线的方向放出一质量为m、带电量-e的电子,发现电子在分界线处速度方向与界线成60°角进入右边磁场,反冲核在管内做匀速直线运动,当到达管另一端Q点时,刚好俘获了这个电子而静止.求: 我国科学家在对放射性元素的研究中,进行了如下实验:如图所示,以MN为界,左、右两边分别是磁感应强度为2B和B的匀强磁场,且磁场区域足够大.在距离界线为l处平行于MN固定一个光滑的瓷管PQ,开始时一个放射性元素的原子核处在管口P处,某时刻该原子核沿平行于界线的方向放出一个质量为m、带电量为-e的电子,发现电子在分界线处以方向与界线成60°角的速度进入右边磁场(如图所示),反冲核在管内匀速直线运动,当到达管另一端Q点时,刚好又俘获了这个电子而静止.求:
我国科学家在对放射性元素的研究中,进行了如下实验:如图所示,以MN为界,左、右两边分别是磁感应强度为2B和B的匀强磁场,且磁场区域足够大.在距离界线为l处平行于MN固定一个光滑的瓷管PQ,开始时一个放射性元素的原子核处在管口P处,某时刻该原子核沿平行于界线的方向放出一个质量为m、带电量为-e的电子,发现电子在分界线处以方向与界线成60°角的速度进入右边磁场(如图所示),反冲核在管内匀速直线运动,当到达管另一端Q点时,刚好又俘获了这个电子而静止.求: 如图所示,以MN为界的两匀强磁场,磁感应强度B1=2B2,方向垂直纸面向里,现有一质量为m、带电量为q的正粒子,从O点沿图示方向进入B1中.
如图所示,以MN为界的两匀强磁场,磁感应强度B1=2B2,方向垂直纸面向里,现有一质量为m、带电量为q的正粒子,从O点沿图示方向进入B1中.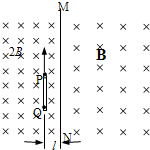 (2005?南通二模)我国科学家在对放射性元素的研究中,进行了如下实验:如图所示,以MN为界,左、右两边分别是磁感应强度为2B和B的匀强磁场,且磁场区域足够大.在距离界线为l处平行于MN固定一个长为s光滑的瓷管PQ,开始时一个放射性元素的原子核处在管口P处,某时刻该原子核平行于界线的方向放出一质量为m、带电量-e的电子,发现电子在分界线处速度方向与界线成60°角进入右边磁场,反冲核在管内匀速直线运动,当到达管另一端Q点时,刚好又俘获了这个电子而静止.求:
(2005?南通二模)我国科学家在对放射性元素的研究中,进行了如下实验:如图所示,以MN为界,左、右两边分别是磁感应强度为2B和B的匀强磁场,且磁场区域足够大.在距离界线为l处平行于MN固定一个长为s光滑的瓷管PQ,开始时一个放射性元素的原子核处在管口P处,某时刻该原子核平行于界线的方向放出一质量为m、带电量-e的电子,发现电子在分界线处速度方向与界线成60°角进入右边磁场,反冲核在管内匀速直线运动,当到达管另一端Q点时,刚好又俘获了这个电子而静止.求: 如图所示,以MN为界的两匀强磁场B1=2B2,一带电+q、质量m的粒子从O点垂直MN进入B1磁场,则经过多长时间它将向下通过O点(不计粒子重力)( )
如图所示,以MN为界的两匀强磁场B1=2B2,一带电+q、质量m的粒子从O点垂直MN进入B1磁场,则经过多长时间它将向下通过O点(不计粒子重力)( )