题目内容
4.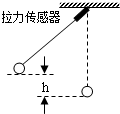 探究小组利用传感器研究小球在摆动过程中的机械能守恒规律,实验装置如图所示.在悬点处装有拉力传感器,可记录小球在摆动过程中各时刻的拉力值.忽略摆线的质量和摆动过程中摆线长度的变化,重力加速度为g,实验过程如下:
探究小组利用传感器研究小球在摆动过程中的机械能守恒规律,实验装置如图所示.在悬点处装有拉力传感器,可记录小球在摆动过程中各时刻的拉力值.忽略摆线的质量和摆动过程中摆线长度的变化,重力加速度为g,实验过程如下:(1)测量小球质量m和摆线长L;
(2)为了测量小球在最低点的速度大小,小组成员将小球拉至某一高度h处无初速释放,在传感器采集的数据中提取最大值为F,则小球在最低点的速度表达式为v=$\sqrt{\frac{(F-mg)L}{m}}$(用F等测定的物理量符号表达),若考虑小球的大小不可忽略,则该速度的计算值与实际值相比较偏小(填写“偏大”、“偏小”或“相等”).
(3)小球从释放到最低点的过程中机械能守恒的表达式为FL=mg(2h+L).(用测定物理量的符号表达)
分析 (2)抓住小球在最低点拉力最大,结合牛顿第二定律求出拉力和速度的关系,从而求出速度大小;若考虑小球的大小,则L将变大,即可判定计算值与实际值的关系;
(3)根据减小的重力势能转化为动能,即可求解.
解答 解:(2)当小球运动到最低点时,拉力最大,根据F-mg=m$\frac{{v}^{2}}{L}$得,
则小球在最低点的速度表达式为v=$\sqrt{\frac{(F-mg)L}{m}}$.
若考虑小球的大小不可忽略,即实际L值变大,而计算时,仍代入L,导致计算值小于实际值,
(3)根据下摆过程中,减小的重力势能转化为动能的增加,即为:mgh=$\frac{1}{2}m{v}^{2}$,
而v=$\sqrt{\frac{(F-mg)L}{m}}$,则有:FL=mg(2h+L)
故答案为:(2)$\sqrt{\frac{(F-mg)L}{m}}$,偏小;(3)FL=mg(2h+L).
点评 考查牛顿第二定律的内容,及向心力表达式,掌握机械能守恒定律的条件,及其应用,注意小球的大小会影响公式中L的值.

练习册系列答案
相关题目
14.氢原子核外只有一个电子,它绕氢原子核运动的角速度为ω=π×1016rad/s,则电子绕核运动的等效电流为( )
| A. | 8×104A | B. | 8×10-4A | C. | 4×104A | D. | 4×10-4A |
19.下列说法正确的是( )
| A. | 对于一定质量的理想气体,体积不变时,温度越高,气体的压强就越大 | |
| B. | 空调机既能致热又能致冷,说明热传递不存在方向性 | |
| C. | 把一枚针放在水面上,它会浮在水面上,这是水表面存在表面张力的缘故 | |
| D. | 分子间的引力和斥力是不能同时存在的,有引力就不会有斥力 | |
| E. | 单晶体的各向异性是由晶体微观结构决定的 |
9.下列有关光的一些现象,说法错误的是( )
| A. | 日光照射在肥皂膜上出现彩色条纹是光的干涉现象 | |
| B. | 雨后出现彩虹是光的色散现象 | |
| C. | 白光通过三棱镜在屏上出现彩色条纹是光的干涉现象 | |
| D. | 汽车前挡风玻璃按同一要求设置,既防止对方强光刺眼,又方便看清前方路面,利用的是光的偏振 |
16.已知地球的第一宇宙速度为7.9km/s,第二宇宙速度为11.2km/s,下列叙述正确的是( )
| A. | 第一宇宙速度是物体在地面附近绕地球做匀速圆周运动的速度 | |
| B. | 第二宇宙速度是成为地球卫星的最小发射速度 | |
| C. | 所有地球卫星环绕地球的运行速度介于7.9km/s和11.2km/s之间 | |
| D. | 宇宙速度是相对于地面,而不是相对地心 |
13.在“蹦床”娱乐活动中,从小朋友下落到离地面高h1处开始计时,其动能EK与离地高度h的关系如图2所示.在h1一h2阶段图象为直线,其余部分为曲线,h3对应图象的最高点,小朋友的质量为m,重力加速度为g,不计空气阻力和一切摩擦.下列有关说法正确的是( )


| A. | 整个过程中小朋友的机械能守恒 | |
| B. | 从小朋友的脚接触蹦床直至蹦床被压缩至最低点的过程中,其加速度先减小后增大 | |
| C. | 小朋友处于h=h4高度时,蹦床的弹性势能为Ep=mg(h2-h4) | |
| D. | 小朋友从h1下降到h5过程中,蹦床的最大弹性势能为EPM=mgh1 |
14.下列四个物理量的表达式中,采用比值定义法的是( )
| A. | 加速度a=$\frac{F}{m}$ | B. | 磁感应强度B=$\frac{F}{IL}$ | C. | 电容C=$\frac{?S}{4πkd}$ | D. | 电场强度E=$\frac{kQ}{{r}^{2}}$ |
 为研究汽车通过桥梁时对凸形、水平、凹形桥面的压力变化,某同学用图1的装置进行模拟实验,将传感器的输出信号接到电脑,从同一高度释放小球,让小球分别通过甲、乙、丙桥面后,电脑屏幕上显示出三条图线(如图2)
为研究汽车通过桥梁时对凸形、水平、凹形桥面的压力变化,某同学用图1的装置进行模拟实验,将传感器的输出信号接到电脑,从同一高度释放小球,让小球分别通过甲、乙、丙桥面后,电脑屏幕上显示出三条图线(如图2) 在光滑绝缘的水平面上,沿x轴0到d范围内存在电场(图中未画出),电场的方向沿x轴正向,并且电场强度大小E随x的分布如图所示.将一质量为m1,电量为+q的小球A,从O点由静止释放.当小球A离开电场后与一个静止且不带电,质量为m2的小球B发生碰撞(设碰撞过程中无机械能损失、小球A、B大小相同,碰撞过程中电荷不发生转移).
在光滑绝缘的水平面上,沿x轴0到d范围内存在电场(图中未画出),电场的方向沿x轴正向,并且电场强度大小E随x的分布如图所示.将一质量为m1,电量为+q的小球A,从O点由静止释放.当小球A离开电场后与一个静止且不带电,质量为m2的小球B发生碰撞(设碰撞过程中无机械能损失、小球A、B大小相同,碰撞过程中电荷不发生转移).