题目内容
5．
内垫光滑的圆管弯成半径相同的两段弧，放在同一竖直圆内如图所示，$\widehat{ADC}$=$\widehat{ABC}$，一小球以某一初速度v0分别沿$\widehat{ADC}$和$\widehat{ABC}$到达C点所需时间分别为t1和t2，则（ ）| A． | t1＞t2 | B． | t1=t2 | C． | t1＜t2 | D． | 无法确定 |
分析 小球沿光滑圆管内运动时机械能守恒，可知小球在C、A两处的速度大小相等，在B点的速度小于D点的速度，分析平均速率关系，即可分析时间关系．
解答 解：小球沿光滑圆管内运动时只有重力做功，其机械能守恒，可知小球在C、A两处的速度大小相等．
由于重力做功，小球从上面经过时的速度要减小，从下面的速度会增大，所以小球在B点的速度小于D点的速度，则知小球沿$\widehat{ADC}$的平均速率大于沿$\widehat{ABC}$的平均速率，而两个过程的路程相等，所以有t1＜t2．
故选：C．
点评 本题要抓住两个过程中平均速率关系，分析时间关系．对于光滑圆管，要知道小球的机械能守恒，运用该定律分析速度的关系．
练习册系列答案
阅读快车系列答案
相关题目
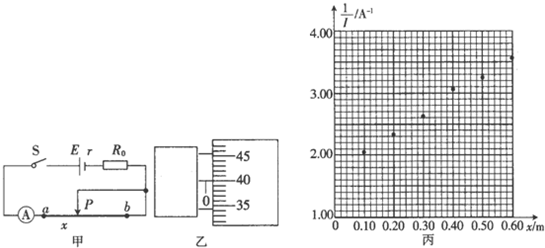
15．为测定一段金属丝的电阻率ρ，某同学设计了如图甲所示的电路．ab是一段电阻率较大的粗细均匀的电阻丝，电路中的保护电阻R0=4.0Ω电源的电动势E=3.0V，电流表内阻忽略不计，滑片P与电阻丝始终接触良好．
（1）实验中用螺旋测微器测得电阻丝的直径如图乙所示，其示数为d=0.400mm．
（2）实验时闭合开关，调节滑片P的位置，分别测量出每次实验中aP长度x及对应的电流值I，实验数据如下表所示：
①表中数据描在$\frac{l}{I}$-x坐标纸中，如图丙所示．试作出其关系图线，图象中直线的斜率的表达式k=$\frac{4ρ}{Eπ{d}^{2}}$（用题中字母表示），由图线求得电阻丝的电阻率ρ2为1.1×10-4Ω•m（保留两位有效数字）．
②根据图丙中$\frac{l}{I}$-x关系图线纵轴截距的物理意义，可求得电源的内阻为1.4Ω（保留两位有效数字）．
（1）实验中用螺旋测微器测得电阻丝的直径如图乙所示，其示数为d=0.400mm．
（2）实验时闭合开关，调节滑片P的位置，分别测量出每次实验中aP长度x及对应的电流值I，实验数据如下表所示：
| x（m） | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| I（A） | 0.49 | 0.43 | 0.38 | 0.33 | 0.31 | 0.38 |
| $\frac{l}{I}$（A-1） | 2.02 | 2.33 | 2.63 | 3.03 | 3.23 | 3.57 |
②根据图丙中$\frac{l}{I}$-x关系图线纵轴截距的物理意义，可求得电源的内阻为1.4Ω（保留两位有效数字）．
如图一条光线平行底边射到截面为等腰直角三角形、折射率为$\sqrt{2}$的玻璃棱镜上，画出光线从入射到第一次出射的光路．
如图所示，一电荷量q=3×10-5C带正电的小球，用绝缘细线悬于竖直放置足够大的平行金属板中的O点．电键S合上后，当小球静止时，细线与竖直方向的夹角α=37°．已知两板相距d=0.1m，电源电动势E=16V，内阻r=1Ω，电阻R1=7Ω，R2=R3=R4=16Ω．g取10m/s2，已知sin37°=0.6，cos37°=0.8．g=10m/S2，求：
20．如图甲，在虚线所示的区域有竖直向上的匀强磁场，面积为S的单匝金属线框放在磁场中，线框上开有一小口与磁场外阻值为R的小灯泡相连．若金属框的总电阻为$\frac{R}{2}$，磁场随时间变化如图乙，下列说法正确的是（ ）
| A． | 感应电流由a向b流过小灯泡 | B． | 线框cd边受到的安培力向左 | ||
| C． | 感应电动势大小为$\frac{{B}_{0}S}{{t}_{0}}$ | D． | ab间电压大小为$\frac{2{B}_{0}S}{3{t}_{0}}$ |
10．
如图所示，电源电动势为E，内阻为r，当可变电阻的滑片P向b点移动时，电压表V1的读数U1与电压表V2的读数U2的变化情况是（ ）
如图所示，电源电动势为E，内阻为r，当可变电阻的滑片P向b点移动时，电压表V1的读数U1与电压表V2的读数U2的变化情况是（ ）| A． | U1变大，U2变小 | B． | U1变大，U2变大 | C． | U1变小，U2变小 | D． | U1变小，U2变大 |
17．
如图所示，在动摩擦因数μ=0.2的水平面上，质量m=2kg的物块与水平轻弹簧相连，物块在与水平方向成θ=45°角的拉力F作用下处于静止状态，此时水平面对物块的弹力恰好为零．g取10m/s2，以下说法正确的是（ ）
如图所示，在动摩擦因数μ=0.2的水平面上，质量m=2kg的物块与水平轻弹簧相连，物块在与水平方向成θ=45°角的拉力F作用下处于静止状态，此时水平面对物块的弹力恰好为零．g取10m/s2，以下说法正确的是（ ）| A． | 此时轻弹簧的弹力大小为20N | |
| B． | 当撤去拉力F的瞬间，物块的加速度大小为8m/s2，方向向右 | |
| C． | 若剪断弹簧，则剪断的瞬间物块的加速度大小为8m/s2，方向向右 | |
| D． | 若剪断弹簧，则剪断的瞬间物块的加速度为0 |
15．
在中间位置有固定转动的长2l轻质杆两端固定两完全相同的质量为m、电荷量为+q的小球1和2，装置放在如图所示的关于数直线对称的电子场中，开始时杆在水平位置静止．现给小球1一个竖直向上的速度，让小球1、2绕转动轴各自转动到B、A位置，A、B间电势差U，小球1、2构成的系统动能减少量是（ ）
在中间位置有固定转动的长2l轻质杆两端固定两完全相同的质量为m、电荷量为+q的小球1和2，装置放在如图所示的关于数直线对称的电子场中，开始时杆在水平位置静止．现给小球1一个竖直向上的速度，让小球1、2绕转动轴各自转动到B、A位置，A、B间电势差U，小球1、2构成的系统动能减少量是（ ）| A． | 一定小于Uq | B． | 一定等于2（Uq+mgl） | C． | 一定大于Uq+mgl | D． | 一定大于$\frac{1}{2}$Uq |