题目内容
如图(a)为一研究电磁感应的实验装置示意图,其中电流传感器(相当于一只理想的电流表)能将各时刻的电流数据实时通过数据采集器传输给计算机,经计算机处理后在屏幕上同步显示出I-t图象.足够长光滑金属轨道电阻不计,倾角θ=30°.轨道上端连接有阻值R=1.0Ω的定值电阻,金属杆MN电阻r=0.5Ω,质量m=0.2kg,杆长L=1m.在轨道区域加一垂直轨道平面向下的匀强磁场,让金属杆从图示位置由静止开始释放,此后计算机屏幕上显示出如图(b)所示的I-t图象(设杆在整个运动过程中与轨道垂直,g=10m/s2).试求:
(1)t=0.5s时电阻R的热功率;
(2)匀强磁场的磁感应强度B的大小;
(3)估算0~1.2s内通过电阻R的电量大小及在R上产生的焦耳热.

(1)t=0.5s时电阻R的热功率;
(2)匀强磁场的磁感应强度B的大小;
(3)估算0~1.2s内通过电阻R的电量大小及在R上产生的焦耳热.

分析:(1)由b图读出t=0.5s时电路中电流,由公式P=I2R求出电阻R的热功率;
(2)由b图读取金属杆达到稳定运动时的电流,此时杆受力平衡,由平衡条件和安培力公式求解磁感应强度B的大小;
(3)通过电阻的电量等于图线与t轴包围的面积大小,估算出图线所包围的面积,即可求得通过电阻的电量,根据法拉第电磁感应定律、欧姆定律得到感应量q=
=
,即可求出杆通过的距离x,根据能量守恒定律求出电路中产生的总热量Q,R上产生的焦耳热QR=
Q.
(2)由b图读取金属杆达到稳定运动时的电流,此时杆受力平衡,由平衡条件和安培力公式求解磁感应强度B的大小;
(3)通过电阻的电量等于图线与t轴包围的面积大小,估算出图线所包围的面积,即可求得通过电阻的电量,根据法拉第电磁感应定律、欧姆定律得到感应量q=
| △Φ |
| R+r |
| BLx |
| R+r |
| R |
| R+r |
解答:解:(1)由I-t图象可知当t=0.5s时,I=1.10A;
P=I2R=1.102×1.0W=1.21W
(2)由图知,当金属杆达到稳定运动时的电流为1.60A,
稳定时杆匀速运动,受力平衡,则有:mgsinθ=BIL
解得B=
=
T=0.625T
(3)1.2s内通过电阻的电量为图线与t轴包围的面积,由图知:
总格数为129格,故q=129×0.1×0.1C=1.29C
由图知:1.2s末杆的电流I=1.50A
由闭合电路欧姆定律得 I=
=
得 v=
=
m/s=3.6m/s
电量q=
△t=
?
=
=
∴x=
=
m=3.096m
根据能量守恒得 mgxsinθ=
mv2+Q
∴电路中产生的总热量为 Q=mgxsinθ-
mv2=(0.2×10×3.096×0.5-
×0.2×3.62)J=1.8J
在R上产生的焦耳热 QR=
Q=
×1.8J=1.2J
答:(1)t=0.5s时电阻R的热功率是1.21W;
(2)匀强磁场的磁感应强度B的大小是0.625T;
(3)0~1.2s内通过电阻R的电量大小是1.29C,在R上产生的焦耳是1.2J.
P=I2R=1.102×1.0W=1.21W
(2)由图知,当金属杆达到稳定运动时的电流为1.60A,
稳定时杆匀速运动,受力平衡,则有:mgsinθ=BIL
解得B=
| mgsinθ |
| IL |
| 0.2×10×0.5 |
| 1.60×1 |
(3)1.2s内通过电阻的电量为图线与t轴包围的面积,由图知:
总格数为129格,故q=129×0.1×0.1C=1.29C
由图知:1.2s末杆的电流I=1.50A
由闭合电路欧姆定律得 I=
| E |
| R+r |
| BLv |
| R+r |
得 v=
| I(R+r) |
| BL |
| 1.50×(1+0.5) |
| 0.625×1 |
电量q=
| E |
| R+r |
| △Φ |
| △t |
| △t |
| R+r |
| △Φ |
| R+r |
| BLx |
| R+r |
∴x=
| q(R+r) |
| BL |
| 1.29×(1+0.5) |
| 0.625×1 |
根据能量守恒得 mgxsinθ=
| 1 |
| 2 |
∴电路中产生的总热量为 Q=mgxsinθ-
| 1 |
| 2 |
| 1 |
| 2 |
在R上产生的焦耳热 QR=
| R |
| R+r |
| 1.0 |
| 1.0+0.5 |
答:(1)t=0.5s时电阻R的热功率是1.21W;
(2)匀强磁场的磁感应强度B的大小是0.625T;
(3)0~1.2s内通过电阻R的电量大小是1.29C,在R上产生的焦耳是1.2J.
点评:本题的难点有两个:一是抓住电流图象“面积”的意义,估算出通过R的电量;二是根据感应电量q=
求出杆通过的距离.
| △Φ |
| R+r |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 社团活动中,某学习小组要探究导电溶液的电阻在体积一定时,其电阻值与长度的关系.现选取一根乳胶管,里面浇灌了盐水,两端用粗铜丝塞住管口,形成一段封闭的盐水柱,进行了如下实验:
社团活动中,某学习小组要探究导电溶液的电阻在体积一定时,其电阻值与长度的关系.现选取一根乳胶管,里面浇灌了盐水,两端用粗铜丝塞住管口,形成一段封闭的盐水柱,进行了如下实验:


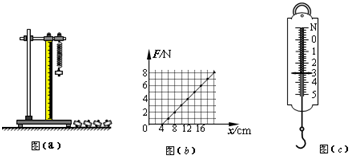 I.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验.
I.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验.