题目内容
2.有3颗质量相同的人造地球卫星,A卫星在地球的赤道上,B卫星为近地卫星,C卫星为地球的同步卫星,比较三卫星所受向心力,线速度,角速度,周期的大小.分析 在赤道上的卫星A与同步卫星C角速度相同,应根据$ω=\frac{2π}{T}$、v=ωr$F=m{ω}_{\;}^{2}r$比较;近地卫星B与同步卫星C根据$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r=m{ω}_{\;}^{2}r$比较.
解答 解:根据$F=m{ω}_{\;}^{2}r$可得${F}_{A}^{\;}<{F}_{C}^{\;}$,由$F=G\frac{Mm}{{r}_{\;}^{2}}$可得${F}_{B}^{\;}>{F}_{C}^{\;}$,所以${F}_{B}^{\;}>{F}_{C}^{\;}>{F}_{A}^{\;}$
根据v=ωr可得,${v}_{A}^{\;}<{v}_{C}^{\;}$,由$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}$可得$v=\sqrt{\frac{GM}{r}}$,即${v}_{B}^{\;}>{v}_{C}^{\;}$,所以${v}_{B}^{\;}>{v}_{C}^{\;}>{v}_{A}^{\;}$
根根据$ω=\frac{2π}{T}$可知,ω与T成反比,所以${ω}_{A}^{\;}={ω}_{C}^{\;}<{ω}_{B}^{\;}$
据题意地球同步卫星C周期${T}_{C}^{\;}$与地球自转周期相同,即与放在赤道的卫星A的周期${T}_{A}^{\;}$相同,即${T}_{C}^{\;}={T}_{A}^{\;}$;对近地卫星B与同步卫星C,由$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$可知,卫星C的周期${T}_{C}^{\;}$应大于卫星B的周期${T}_{B}^{\;}$,${T}_{C}^{\;}>{T}_{B}^{\;}$,所以${T}_{A}^{\;}={T}_{C}^{\;}>{T}_{B}^{\;}$
答:三卫星向心力${F}_{B}^{\;}>{F}_{C}^{\;}>{F}_{A}^{\;}$;线速度${v}_{B}^{\;}>{v}_{C}^{\;}>{v}_{A}^{\;}$;角速度${ω}_{A}^{\;}={ω}_{C}^{\;}<{ω}_{B}^{\;}$;周期${T}_{A}^{\;}={T}_{C}^{\;}>{T}_{B}^{\;}$
点评 注意卫星做圆周运动需要的向心力全部由万有引力提供,而赤道上的物体随地球自转需要的向心力只是万有引力的很小一部分来提供,特别注意同步卫星与赤道上物体向心力来源的不同.

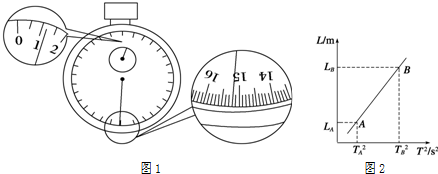
 如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置.连续两次曝光的时间间隔均为T,每块砖的厚度为d,根据图中的信息,下列判断错误的是( )
如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置.连续两次曝光的时间间隔均为T,每块砖的厚度为d,根据图中的信息,下列判断错误的是( )| A. | 小球释放的初始位置在“1”上方d距离处 | |
| B. | 小球做匀加速直线运动 | |
| C. | 小球下落的加速度为$\frac{d}{{T}^{2}}$ | |
| D. | 小球通过位置“3”和“4”的平均速度为$\frac{4d}{T}$ |
| A. | 电子 | B. | 中子 | C. | 质子 | D. | 原子核 |
 研究放射性元素射线性质的实验装置如图所示.两块平行放置的金属板A、B分别于电源的两极a、b连接,放射源发出的射线从其上方小孔向外射出.则( )
研究放射性元素射线性质的实验装置如图所示.两块平行放置的金属板A、B分别于电源的两极a、b连接,放射源发出的射线从其上方小孔向外射出.则( )| A. | a为电源正极,到达A板的为α射线 | B. | a为电源正极,到达A板的为β射线 | ||
| C. | a为电源负极,到达A板的为α射线 | D. | a为电源负极,到达A板的为β射线 |
| A. | υ向上,a向下 | B. | υ向上,a为零 | C. | υ向下,a向下 | D. | υ向下,a为零. |
 如图所示,一足够长的光滑斜面上,质量为5千克的物体,静止在底端的A点,现用大小为F=50N,方向平行于斜面的拉力沿斜开始向上拉,到达B点时撤去拉力F,已知AB=8m,倾角θ=37°,g=10m/s2,求:
如图所示,一足够长的光滑斜面上,质量为5千克的物体,静止在底端的A点,现用大小为F=50N,方向平行于斜面的拉力沿斜开始向上拉,到达B点时撤去拉力F,已知AB=8m,倾角θ=37°,g=10m/s2,求: (1)杨氏干涉实验证明光的确是一种波,一束单色光投射在两条相距很近的狭缝上,两狭缝就成了两个光源,它们发出的光波满足干涉的必要条件,则两列光的频率相同.如图所示,在这两列光波相遇的区域中,实线表示波峰,虚线表示波谷,如果放置光屏,在C(选填“A”、“B”或“C”)点会出现暗条纹.
(1)杨氏干涉实验证明光的确是一种波,一束单色光投射在两条相距很近的狭缝上,两狭缝就成了两个光源,它们发出的光波满足干涉的必要条件,则两列光的频率相同.如图所示,在这两列光波相遇的区域中,实线表示波峰,虚线表示波谷,如果放置光屏,在C(选填“A”、“B”或“C”)点会出现暗条纹.