题目内容
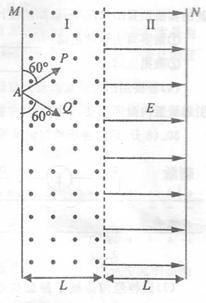
如图所示,真空室内竖直条形区域I存在垂直纸面向外的匀强磁场,条形区 域II(含I、II区域分界面)存在水平向右的勻强电场,电场强度为E,磁场和电场宽度均为 L,高度足够大,M、N为涂有荧光物质的竖直板。现有P、Q两束质子从A处连续不断地射 入磁场,入射方向都与M板成60°夹角且与纸面平行,两束质子束的速度大小都恒为v。当 I区中磁场较强时,M板上有一个亮斑,N板上无亮斑。缓慢改变磁场强弱,M板和N板 上会各有一个亮斑,继续改变磁场强弱,可以观察到N板出现两个亮斑时,M板上的亮斑阐 好消失。已知质子质量为m,电量为e,不计质子重力和相互作用力,求:
(1) N板上刚刚出现一个亮斑时,M板上的亮斑到 A点的距离x;
(2) N板上恰好出现两个亮斑时,区域I中的磁感 应强度B;
(3)N板上恰好出现两个亮斑时,这两个亮斑之间 的距离s。
(1)N板上恰出现一个亮斑时,两束质子的轨迹如图所示,设轨迹的半径为R.
有 R+Rsin30°=L (2分)
而 x=![]() (2分)
(2分)
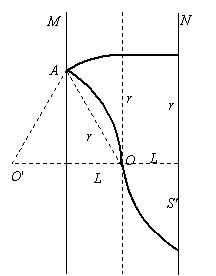
(2)N板上恰好出现两个亮斑时,两束质子的轨迹如
右图所示。设轨迹半径为r。有
rsin30°=L (2分)
evB=mv2/r (2分)
解得 B=mv/(2eL) (2分)
(3)质子束P恰垂直进入电场区域,质子束Q恰在O点以垂直电场的速度进入电场。(2分)
L=![]() (2分)
(2分)
s' =vt (2分)
s=r+ s' =2L+![]() (2分)
(2分)
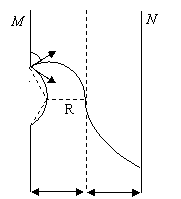 |

练习册系列答案
相关题目
 如图所示,真空室内竖直条形区域I存在垂直纸面向外的匀强磁场,条形区域Ⅱ(含I、Ⅱ区域分界面)存在水平向右的匀强电场,电场强度为E,磁场和电场宽度均为L且足够长,M、N为涂有荧光物质的竖直板.现有一束质子从A处连续不断地射入磁场,入射方向与M板成60°夹角且与纸面平行如图,质子束由两部分组成,一部分为速度大小为v的低速质子,另一部分为速度大小为3v的高速质子,当I区中磁场较强时,M板出现两个亮斑,缓慢改变磁场强弱,直至亮斑相继刚好消失为止,此时观察到N板有两个亮斑.已知质子质量为m,电量为e,不计质子重力和相互作用力,求:
如图所示,真空室内竖直条形区域I存在垂直纸面向外的匀强磁场,条形区域Ⅱ(含I、Ⅱ区域分界面)存在水平向右的匀强电场,电场强度为E,磁场和电场宽度均为L且足够长,M、N为涂有荧光物质的竖直板.现有一束质子从A处连续不断地射入磁场,入射方向与M板成60°夹角且与纸面平行如图,质子束由两部分组成,一部分为速度大小为v的低速质子,另一部分为速度大小为3v的高速质子,当I区中磁场较强时,M板出现两个亮斑,缓慢改变磁场强弱,直至亮斑相继刚好消失为止,此时观察到N板有两个亮斑.已知质子质量为m,电量为e,不计质子重力和相互作用力,求: (2013?郑州二模)如图所示,真空室内竖直条形区域I存在垂直纸面向外的匀强磁场、条形区域Ⅱ(含Ⅰ、Ⅱ区域分界面)存在水平向右的匀强电场,电场强度为E,磁场和电场宽度均为L,高度足够大,M、N为涂有荧光物质的竖直板.现有P、Q两束质子从A处连续不断地射入磁场,入射方向都与M板成60°夹角且与纸面平行,两束质子束的速度大小都恒为v.当Ⅰ区中磁场较强时,M板上有一个亮斑,N板上无亮斑.缓慢改变磁场强弱,M板和N板上会各有一个亮斑,继续改变磁场强弱,可以观察到N板出现两个亮斑时,M板上的亮斑刚好消失.已知质子质量为m,电量为e,不计质子重力和相互作用力,求:
(2013?郑州二模)如图所示,真空室内竖直条形区域I存在垂直纸面向外的匀强磁场、条形区域Ⅱ(含Ⅰ、Ⅱ区域分界面)存在水平向右的匀强电场,电场强度为E,磁场和电场宽度均为L,高度足够大,M、N为涂有荧光物质的竖直板.现有P、Q两束质子从A处连续不断地射入磁场,入射方向都与M板成60°夹角且与纸面平行,两束质子束的速度大小都恒为v.当Ⅰ区中磁场较强时,M板上有一个亮斑,N板上无亮斑.缓慢改变磁场强弱,M板和N板上会各有一个亮斑,继续改变磁场强弱,可以观察到N板出现两个亮斑时,M板上的亮斑刚好消失.已知质子质量为m,电量为e,不计质子重力和相互作用力,求:

