题目内容
11.不计空气阻力,以一定的初速度竖直上抛一物体,从抛出至回到抛出点的时间为t,上升的最大高度为h.现在距物体抛出点$\frac{3}{4}$h处设置一块挡板,物体撞击挡板后的速度大小减为0,撞击所需时间不计,则这种情况下物体上升和下降的总时间约为( )| A. | 0.4t | B. | 0.5t | C. | 0.6t | D. | 0.7t |
分析 由竖直上抛运动的速度公式与位移公式求出第一次时的时间与高度的关系,然后由位移公式分别求出上升与下降的时间,最后求和即可.
解答 解:物体下降时间为0.5t,故高度为:h=$\frac{1}{2}g$($\frac{t}{2}$)2
物体自由落体运动$\frac{1}{4}$h过程,有:
$\frac{1}{4}h$=$\frac{1}{2}gt{′}^{2}$
物体到挡板处
t′=$\sqrt{\frac{h}{2g}}$=0.25t
从挡板处落地的时间:
t″=$\sqrt{\frac{2×\frac{3}{4}h}{g}}$≈0.433t
故第二次物体上升和下降的总时间:t下=t′+t″=0.25t+0.433t=0.683t≈0.7t.所以选项D正确
故选:D
点评 本题关键抓住竖直上抛运动的对称性进行分析,竖直上抛运动的上升阶段和下降各阶段具有严格的对称性.
(1)速度对称:物体在上升过程和下降过程中经过同一位置时速度大小相等,方向相反.
(2)时间对称:物体在上升过程和下降过程中经过同一段高度所用的时间相等.
(3)能量对称:物体在上升过程和下降过程中经过同一段高度重力势能变化量的大小相等,均为mgh.
物体第二次运动依然具有对称性,上升和下降时间相等;根据位移时间关系公式列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图所示,两物体A、B的质量分别为M和m,用跨过定滑轮的轻绳相连,物体A静止在粗糙水平面上,细线与水平方向的夹角为θ,B悬停于空中.若不计细线与滑轮间的摩擦,重力加速度为g.则( )
如图所示,两物体A、B的质量分别为M和m,用跨过定滑轮的轻绳相连,物体A静止在粗糙水平面上,细线与水平方向的夹角为θ,B悬停于空中.若不计细线与滑轮间的摩擦,重力加速度为g.则( )
 如图所示,两物体A、B的质量分别为M和m,用跨过定滑轮的轻绳相连,物体A静止在粗糙水平面上,细线与水平方向的夹角为θ,B悬停于空中.若不计细线与滑轮间的摩擦,重力加速度为g.则( )
如图所示,两物体A、B的质量分别为M和m,用跨过定滑轮的轻绳相连,物体A静止在粗糙水平面上,细线与水平方向的夹角为θ,B悬停于空中.若不计细线与滑轮间的摩擦,重力加速度为g.则( )| A. | 地面对物体A的支持力大小等于Mg-mgsinθ | |
| B. | 物体A对地面的压力大小等于Mg | |
| C. | 物体A与地面之间的动摩擦因数等于$\frac{mgcosθ}{Mg-mgsinθ}$ | |
| D. | 物体A所受摩擦力大小等于0 |
19.如图所示,电荷+Q附近有一点电荷q逐渐向它靠近的过程中,以下结论正确的是( )


| A. | 若为+q,则q的受力越来越大,速度越来越大 | |
| B. | 若为+q,则q的受力越来越大,速度越来越小 | |
| C. | 若为-q,则q的受力越来越小,速度越来越大 | |
| D. | 若为-q,则q的受力越来越大,速度越来越大 |
3. 如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,下列说法正确的是( )
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,下列说法正确的是( )
 如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,下列说法正确的是( )
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,下列说法正确的是( )| A. | 小球电势能的减少量大于小球重力势能的增加量 | |
| B. | 弹簧弹性势能的增加量等于小球动能的减少量 | |
| C. | 小球机械能的改变量等于电场力做的功 | |
| D. | 小球动能的减少量等于电场力和重力做功的代数和 |
20.下列有关科学家的贡献说法正确的是( )
| A. | 卡文迪许发现了万有引力定律 | |
| B. | 奥斯特首先提出用电场线来描绘电场 | |
| C. | 密立根通过对摩擦起电的研究测定了元电荷的电荷量 | |
| D. | 麦克斯韦建立了电磁场理论,并提出光也是一种电磁波 |
4. 在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )
在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )
 在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )
在真空中同一直线上的A、B处分别固定电量分别为+2Q、-Q的两电荷.如图所示,若在A、B所在直线上放入第三个电荷C,只在电场力作用下三个电荷都处于平衡状态,则C的电性及位置是( )| A. | 正电,在A、B之间 | B. | 正电,在B点右侧 | C. | 负电,在B点右侧 | D. | 负电,在A点左侧 |
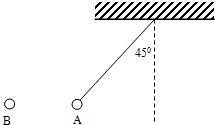 如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时
如图所示,把质量为0.2g的带电小球A用丝线吊起,若将带电荷量为4×10-8C的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时