题目内容
5. 如图所示,一辆平板车上竖直固定着一个光滑的$\frac{1}{4}$圆弧轨道,轨道半径为R,道与平板相切于A,车的平板部分粗糙,轨道与车的总质量为M,若将平板车放在光滑水平上,初始时车静止,一个质量为m的球(不计大小)从圆弧轨道顶端滑下,当它到达平板车B点时,与车相对静止,已知AB=s,求在此过程中,车对地的位移有多大?
如图所示,一辆平板车上竖直固定着一个光滑的$\frac{1}{4}$圆弧轨道,轨道半径为R,道与平板相切于A,车的平板部分粗糙,轨道与车的总质量为M,若将平板车放在光滑水平上,初始时车静止,一个质量为m的球(不计大小)从圆弧轨道顶端滑下,当它到达平板车B点时,与车相对静止,已知AB=s,求在此过程中,车对地的位移有多大?
分析 平板车和小球组成的系统水平方向不受外力,系统的动量守恒,由动量守恒定律和速度与位移的关系求解.
解答 解:设在此过程中,车对地的位移大小为x.则小球对地的位移大小为R+s-x.
取向右为正方向,根据动量守恒定律得:m$\frac{R+s-x}{t}$-M$\frac{x}{t}$=0
解得:x=$\frac{m(R+s)}{M+m}$
答:在此过程中,车对地的位移为$\frac{m(R+s)}{M+m}$.
点评 对于小球在小车滑行的过程,要明确系统的总动量不守恒,只是水平方向动量守恒.运用平均动量守恒研究小车的位移.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
10.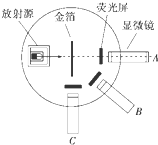 如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
 如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )| A. | 相同时间内放在A位置时观察到屏上的闪光次数最少 | |
| B. | 相同时间内放在B位置时观察到屏上的闪光次数最少 | |
| C. | 相同时间内放在C位置时观察到屏上的闪光次数最少 | |
| D. | 放在C位置时观察不到屏上有闪光 |
17.两个共点力,一个是40N,另一个未知,合力大小是100N,则另一个力可能是( )
| A. | 20 N | B. | 40 N | C. | 80 N | D. | 140 N |
14.在下列图象中,描述质点做匀速直线运动的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图是探究电磁感应现象的实验装置,请写出能产生感应电流的两种操作方法:
如图是探究电磁感应现象的实验装置,请写出能产生感应电流的两种操作方法:
 如图所示,水平面上有一物体,人通过定滑轮用绳子拉它,在图示位置时,若人的速度为5m/s,则物体的瞬时速度为多少?
如图所示,水平面上有一物体,人通过定滑轮用绳子拉它,在图示位置时,若人的速度为5m/s,则物体的瞬时速度为多少?