题目内容
如图所示，一水池深为h，一根长直木棍竖直地插入水底，棍露出水面部分的长度为L，当太阳光与水平面夹角为60°斜射到水面时，已知水的折射率为n，求棍在水底的影子的长度．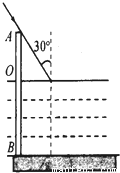
【答案】分析：作出光路图，画出棍在水底的影子，由折射率n=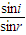
求出折射角，根据几何知识求出影子的长度．
解答：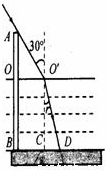
解：依题意画出如图所示的示意图，影子长为BD．AO长为L，因∠AO'O=60°，所以
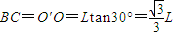
因为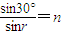
所以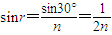
，
则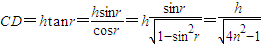
所以水底的影子长为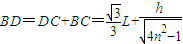
．
答：水底的影子长为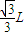
+
．
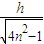点评：本题画出光路图，作出影子，由折射定律和几何关系结合求解影子的长度．
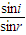求出折射角，根据几何知识求出影子的长度．解答：
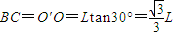
解：依题意画出如图所示的示意图，影子长为BD．AO长为L，因∠AO'O=60°，所以因为
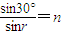
所以
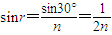，则
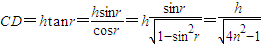
所以水底的影子长为
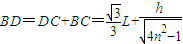．答：水底的影子长为
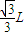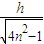+．点评：本题画出光路图，作出影子，由折射定律和几何关系结合求解影子的长度．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
（2012?洛阳模拟）如图所示，一水池深为h，一根长直木棍竖直地插入水底，棍露出水面部分的长度为L，当太阳光与水平面夹角为60°斜射到水面时，已知水的折射率为n，求棍在水底的影子的长度．
斜射到水面时，已知水的折射率为n，求棍在水底的影子的长度．
斜射到水面时，则棍在水底的影子的长度为 ． (已知水的折射率为n)
斜射到水面时，则棍在水底的影子的长度为 ． (已知水的折射率为n)