题目内容
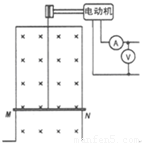
如图所示,电动机牵引一根原来静止的、长L为0.4m、质量m为0.2kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直.当导体棒上升h=1.5m时,获得稳定的速度,导体棒上产生的热量为1.2J,电动机牵引棒时,电压表、电流表的读数分别为7V、1.2A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求:(1)棒能达到的稳定速度;
(2)棒从静止至达到稳定速度所需要的时间.
【答案】分析:(1)金属棒在电动机的牵引下从静止运动一定距离后匀速运动,达到稳定速度,并产生了焦耳热.而由电动机的输入电压、电流再结合线圈内阻可求出电动的输出功率.则由能量守恒定律可算出稳定速度大小.
(2)金属棒从静止到稳定速度做非匀加速运动,则可运用动能定理求出所需要的时间.
解答:解:(1)电动机的输出功率为: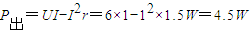
电动机的输出功率就是电动机牵引棒的拉力的功率,所以有P出=Fv
其中F为电动机对棒的拉力,当棒达稳定速度时F=mg+BI'L
感应电流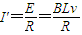
由上述三式得,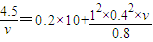
解得棒达到的稳定速度为v≈1.9m/s
(2)从棒由静止开始运动至达到稳定速度的过程中,电动机提供的能量转化为棒的机械能和内能,由能量守恒定律得:
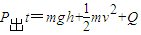
代入得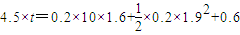
解得:t=0.92s
答:
(1)棒能达到的稳定速度是1.9m/s;
(2)棒从静止至达到稳定速度所需要的时间是0.92s.
点评:本题关键要抓住金属棒稳定状态,从电动机的输入功率减去电动线圈消耗的功率等于电动机输出功率.在金属棒上升过程中由于非匀加速,故不能用运动学公式求出,则选择动能定理.
(2)金属棒从静止到稳定速度做非匀加速运动,则可运用动能定理求出所需要的时间.
解答:解:(1)电动机的输出功率为:
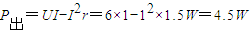
电动机的输出功率就是电动机牵引棒的拉力的功率,所以有P出=Fv
其中F为电动机对棒的拉力,当棒达稳定速度时F=mg+BI'L
感应电流
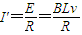
由上述三式得,
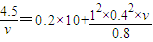
解得棒达到的稳定速度为v≈1.9m/s
(2)从棒由静止开始运动至达到稳定速度的过程中,电动机提供的能量转化为棒的机械能和内能,由能量守恒定律得:
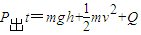
代入得
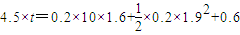
解得:t=0.92s
答:
(1)棒能达到的稳定速度是1.9m/s;
(2)棒从静止至达到稳定速度所需要的时间是0.92s.
点评:本题关键要抓住金属棒稳定状态,从电动机的输入功率减去电动线圈消耗的功率等于电动机输出功率.在金属棒上升过程中由于非匀加速,故不能用运动学公式求出,则选择动能定理.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
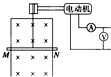 如图所示,电动机牵引一根原来静止的、长L为1m、质量m为0.1kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直.当导体棒上升h=3.8m时,获得稳定的速度,导体棒上产生的热量为2J,电动机牵引棒时,电压表、电流表的读数分别为7V、1A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,则以下判断正确的是( )
如图所示,电动机牵引一根原来静止的、长L为1m、质量m为0.1kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直.当导体棒上升h=3.8m时,获得稳定的速度,导体棒上产生的热量为2J,电动机牵引棒时,电压表、电流表的读数分别为7V、1A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,则以下判断正确的是( )| A、导体棒向上做匀减速运动 | B、电动机的输出功率为49J | C、导体棒达到稳定时的速度为v=2m/s | D、导体棒从静止至达到稳定速度所需要的时间为1s |
 如图所示,电动机牵引的是一根原来静止的长L=1m,质量m=0.1kg的金属棒MN,棒电阻R=1Ω,MN架在处于磁感强度B=1T的水平匀强磁场中的竖直放置的固定框架上,磁场方向与框架平面垂直,当导体棒上升h=3.8m时获得稳定速度,其产生的焦耳热Q=2J,电动机牵引棒时,伏特表、安培表的读数分别为7V、1A,已知电动机的内阻r=1Ω,不计框架电阻及一切摩擦,g取10m/s2,求:
如图所示,电动机牵引的是一根原来静止的长L=1m,质量m=0.1kg的金属棒MN,棒电阻R=1Ω,MN架在处于磁感强度B=1T的水平匀强磁场中的竖直放置的固定框架上,磁场方向与框架平面垂直,当导体棒上升h=3.8m时获得稳定速度,其产生的焦耳热Q=2J,电动机牵引棒时,伏特表、安培表的读数分别为7V、1A,已知电动机的内阻r=1Ω,不计框架电阻及一切摩擦,g取10m/s2,求: 如图所示,电动机牵引的是一根原来静止的长L=1m、质量m=0.1kg的金属棒MN,棒电阻R=1Ω,金属棒MN架在处于磁感强度B=1T的水平匀强磁场中的竖直放置的固定框架上,磁场方向与框架平面垂直,当导体棒上升一定高度后获得稳定速度.电动机牵引棒时,电压表、电流表的读数分别为7V和1A.已知电动机内阻r=1Ω,不计框架电阻及一切摩擦,求:金属棒所达到的稳定速度的大小.
如图所示,电动机牵引的是一根原来静止的长L=1m、质量m=0.1kg的金属棒MN,棒电阻R=1Ω,金属棒MN架在处于磁感强度B=1T的水平匀强磁场中的竖直放置的固定框架上,磁场方向与框架平面垂直,当导体棒上升一定高度后获得稳定速度.电动机牵引棒时,电压表、电流表的读数分别为7V和1A.已知电动机内阻r=1Ω,不计框架电阻及一切摩擦,求:金属棒所达到的稳定速度的大小. 如图所示,电动机牵引一根原来静止的、长L为1m、质量m为0.1kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直.当导体棒上升h=3.8m时,获得稳定的速度,导体棒上产生的热量为2J,电动机牵引棒时,电压表、电流表的读数分别为7V、1A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求:
如图所示,电动机牵引一根原来静止的、长L为1m、质量m为0.1kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直.当导体棒上升h=3.8m时,获得稳定的速度,导体棒上产生的热量为2J,电动机牵引棒时,电压表、电流表的读数分别为7V、1A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求: (2011?黄浦区一模)如图所示,电动机牵引一根原来静止的、长L为0.4m、质量m为0.2kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直.当导体棒上升h=1.5m时,获得稳定的速度,导体棒上产生的热量为1.2J,电动机牵引棒时,电压表、电流表的读数分别为7V、1.2A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求:
(2011?黄浦区一模)如图所示,电动机牵引一根原来静止的、长L为0.4m、质量m为0.2kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直.当导体棒上升h=1.5m时,获得稳定的速度,导体棒上产生的热量为1.2J,电动机牵引棒时,电压表、电流表的读数分别为7V、1.2A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求: