题目内容
20. 2011年3月10日12时58分云南盈江发生了5.8级地震.在抗震救灾中,我国自主研制的“北斗一号“卫星导航系统,在抗震救灾中发挥了巨大作用.北斗导航系统又被称为“双星定位系统“,具有导航、定位等功能.“北斗“系统中两颗工作星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的AB两位置 (如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列判断中正确的是( )
2011年3月10日12时58分云南盈江发生了5.8级地震.在抗震救灾中,我国自主研制的“北斗一号“卫星导航系统,在抗震救灾中发挥了巨大作用.北斗导航系统又被称为“双星定位系统“,具有导航、定位等功能.“北斗“系统中两颗工作星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的AB两位置 (如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列判断中正确的是( )| A. | 这两颗卫星的加速度大小相等,均为$\frac{{R}^{2}g}{{r}^{2}}$ | |
| B. | 卫星1向后喷气就一定能追上卫星2 | |
| C. | 卫星1由位置A运动至位置B所需的时间为$\frac{πr}{R}$$\sqrt{\frac{r}{g}}$ | |
| D. | 卫星1由位置A运动到位置B的过程中万有引力做功为零 |
分析 由 $\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=m$\frac{{4π}^{2}r}{{T}^{2}}$可得出r相同则速度v大小相等,v变大则r变大(做离心运动),再结合 $\frac{GMm}{{R}^{2}}$=mg即GM=gR2(黄金代换),即可求解.
解答 解:A、根据F=ma得,对卫星有
$\frac{GMm}{{r}^{2}}$=ma,
可得a=$\frac{GM}{{r}^{2}}$,取地面一物体由$\frac{GMm}{{R}^{2}}$=mg
联立解得a=$\frac{{R}^{2}g}{{r}^{2}}$,故A正确.
B、若卫星1向后喷气,则其速度会增大,卫星1将做离心运动,所以卫星1不可能追上卫星2.故B错误
C、根据$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}r}{{T}^{2}}$,
T=2π$\sqrt{\frac{{r}^{3}}{GM}}$…①,
又GM=gR2…②,
t=$\frac{1}{6}$T…③,
联立①②③可解得:t=$\frac{πr}{3R}$$\sqrt{\frac{r}{g}}$,故C错误
D、卫星1由位置A运动到位置B的过程中,由于万有引力始终与速度垂直,故万有引力不做功,故D正确.
故选:AD.
点评 关于做圆周运动的卫星类问题,要灵活运用两个公式$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=m$\frac{{4π}^{2}r}{{T}^{2}}$以及$\frac{GMm}{{R}^{2}}$=mg,注意卫星若加速则做离心运动,减速则做向心运动.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.在地月系统中,若忽略其它星球的影响,可将月球和地球看成双星系统,即它们在彼此引力作用下绕二者连线上的某点做匀速圆周运动.设想人类能够在月球行生活,为了减轻地球上人口太多的压力,可以不断将人送到月球上居住,假设月球和地球间的距离不变,它们的轨道可看成圆,则在该过程中,下列说法正确的是( )
| A. | 月球做圆周运动的角速度不断增大 | B. | 月球做圆周运动的角速度不断减小 | ||
| C. | 地球做圆周运动的轨道半径增大 | D. | 地球做圆周运动的轨道半径减小 |
12.根据《中国广播电视报》报道,在暑天就诊的小病人,低锌发病率高达60%以上.由于锌对人体代谢起着重要作用,因此儿童生长发育时期测量体内含锌量已成为体格检查的重要内容之一,也引起了我国科技工作者的高度重视.其中比较简单的一种检测方法是取儿童的头发约50g,放在核反应堆中经中子轰击后,头发中的锌元素与中子反应生成具有放射性的同位素锌,其核反应方程式为${\;}_{30}^{64}$Zn+${\;}_{0}^{1}$n→${\;}_{30}^{65}$Zn.${\;}_{30}^{65}$Zn衰变放射出能量为1115eV的γ射线,通过测定γ射线的强度可以计算出头发中锌的含量.关于以上叙述,下列说法正确的是( )
| A. | ${\;}_{30}^{64}$Zn和${\;}_{30}^{65}$Zn有相同的核子数 | |
| B. | ${\;}_{30}^{64}$Zn和${\;}_{30}^{65}$Zn具有相同的质子数 | |
| C. | γ射线具有很强的穿透能力,能穿透几厘米的铅板 | |
| D. | γ射线在真空中传播的速度是3.0×108m/s |

 如图是小强测绘小灯泡伏安特性曲线的实物图.小强在实验前检查电路时发现有一根导线的一端接错了地方,请你将图中的这根连线画上“×”,并在图上画出这根导线的正确连线;闭合开关前应将滑动变阻器的触动头滑到最左端(填“最左端”或“最右端”);该实验采用了电流表的外接法(选填“内接”或“外接”).
如图是小强测绘小灯泡伏安特性曲线的实物图.小强在实验前检查电路时发现有一根导线的一端接错了地方,请你将图中的这根连线画上“×”,并在图上画出这根导线的正确连线;闭合开关前应将滑动变阻器的触动头滑到最左端(填“最左端”或“最右端”);该实验采用了电流表的外接法(选填“内接”或“外接”). 如图所示,一传送皮带与水平面夹角为α=37°,正以2m/s的恒定速率顺时针运行.现将一质量为10kg的工件轻放于其底端,经一段时间送到高3m的平台上,已知工件与皮带间的动摩擦因数为μ=$\frac{7}{8}$,g取10m/s2,求带动皮带的电动机由于传送工件多消耗的电能.
如图所示,一传送皮带与水平面夹角为α=37°,正以2m/s的恒定速率顺时针运行.现将一质量为10kg的工件轻放于其底端,经一段时间送到高3m的平台上,已知工件与皮带间的动摩擦因数为μ=$\frac{7}{8}$,g取10m/s2,求带动皮带的电动机由于传送工件多消耗的电能. 如图所示,在离地面H=5.45m的O处用长L=0.45m的不可伸长的细线挂一质量为90g的爆竹(火药质量忽略不计),把爆竹拉起至D点使细线水平伸直,点燃导火线后将爆竹无初速度释放,爆竹刚好到达最低点B时炸成质量相等的两块,一块朝相反方向水平抛出,落到地面上的A处,抛出的水平距离S=5m.另一块仍系在细线上继续做圆周运动并通过最高点C.假设火药爆炸释放的能量全部转化为爆竹碎片的动能,空气阻力忽略不计,取g=10m/s2,求:
如图所示,在离地面H=5.45m的O处用长L=0.45m的不可伸长的细线挂一质量为90g的爆竹(火药质量忽略不计),把爆竹拉起至D点使细线水平伸直,点燃导火线后将爆竹无初速度释放,爆竹刚好到达最低点B时炸成质量相等的两块,一块朝相反方向水平抛出,落到地面上的A处,抛出的水平距离S=5m.另一块仍系在细线上继续做圆周运动并通过最高点C.假设火药爆炸释放的能量全部转化为爆竹碎片的动能,空气阻力忽略不计,取g=10m/s2,求: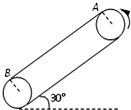 如图所示,皮带传动装置与水平面夹角为30°,轮半径R=$\frac{1}{4π}$m,两轮轴心相距L=8.15m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑,一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$.小物块相对于传送带运动时,会在传送带上留下痕迹.当传送带沿逆时针方向匀速运动时,小物块无初速地放在A点,运动至B点飞出.若传送带沿逆时针方向匀速运动的速度v0=1.5m/s,求划痕的长度?
如图所示,皮带传动装置与水平面夹角为30°,轮半径R=$\frac{1}{4π}$m,两轮轴心相距L=8.15m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑,一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$.小物块相对于传送带运动时,会在传送带上留下痕迹.当传送带沿逆时针方向匀速运动时,小物块无初速地放在A点,运动至B点飞出.若传送带沿逆时针方向匀速运动的速度v0=1.5m/s,求划痕的长度?