题目内容
1.匝数为n的圆形线圈半径为b,内接正方形磁形区域EFGH.通过如图(甲)所示的电路连接到平行板电极M、N.两板间的距离为l,电路中连接的电阻阻值为R.当t=0时,一质量为m,电量为q的带正电微粒(不计重力)以初速度v0从M板垂直射入两板间,微粒和极板接触后不再反弹.已知圆形线圈的电阻为r,导线电阻忽略不计.磁场区域的磁感应强度的变化图线如图乙所示.求:(1)通过电阻R的电流大小、方向以及R上产生的热量;
(2)微粒在电场作用下的加速度大小和方向;
(3)若微粒最后与M极板碰撞,求电场力做的功(为简化表达,把微粒在电场力作用下的加速度大小为a作已知).

分析 (1)根据几何关系确定正方形区域的面积,再根据法拉第电磁感应定律与闭合电路欧姆定律,及楞次定律与焦耳定律,即可求解;
(2)根据U=IR公式,求得MN两端电压,再结合牛顿第二定律,即可求解加速度大小,再由电场强度方向与电荷的电性,从而确定加速度方向;
(3)根据运动的时间,来分打到与没打到情况,没打到的电场力做功为零,而打到的,根据功的表达式,结合运动学公式,求得位移,从而求解.
解答 解:(1)由几何关系可得,磁场区域的边长为$\sqrt{2}$b,面积S=2b2;
由图象可知,磁感应强度的变化率为:$\frac{△B}{△t}$=$\frac{{B}_{0}}{{t}_{0}}$;
线圈内产生的感应电动势为:E=n$\frac{△∅}{△t}$=n$\frac{△B}{△t}$=$\frac{2n{B}_{0}{b}^{2}}{{t}_{0}}$;
所以通过R的电流为:I=$\frac{E}{R+r}$=$\frac{2n{B}_{0}{b}^{2}}{(R+r){t}_{0}}$
根据楞次定律可知,感应电流方向:C→D;
由焦耳定律,那么R上产生热量为:Q=I2Rt0=$\frac{4{n}^{2}R{{B}_{0}}^{2}{b}^{4}}{(R+r)^{2}{t}_{0}}$;
(2)MN两端的电势差为:U=IR=$\frac{2nR{B}_{0}{b}^{2}}{(r+R){t}_{0}}$
微粒在两板间的加速度为:a=$\frac{qU}{ml}$=$\frac{2nqR{B}_{0}{b}^{2}}{ml(r+R){t}_{0}}$;
由于微粒带正电,且左极板电势低于右板,因此方向垂直极板向左,
(3)微粒匀减速直到速度为零所用时间为t,则有:t=$\frac{{v}_{0}}{a}$;
①若2t≤t0,则有电场力做功为零;
②若2t≥t0,减速直到零的位移为:s1=$\frac{1}{2}a{t}^{2}$,
再在(t0-t)时间内反向加速的位移为:s2=$\frac{1}{2}a({t}_{0}-t)^{2}$;
可得电场力做功为:W=-F(s1-s2)=ma$•\frac{1}{2}a(({t}_{0}-t)^{2}-{t}^{2})$=$\frac{1}{2}ma{t}_{0}(a{t}_{0}-{v}_{0})$
答:(1)通过电阻R的电流大小$\frac{2n{B}_{0}{b}^{2}}{(R+r){t}_{0}}$、方向C→D以及R上产生的热量$\frac{4{n}^{2}R{{B}_{0}}^{2}{b}^{4}}{(R+r)^{2}{t}_{0}}$;
(2)微粒在电场作用下的加速度大小$\frac{2nqR{B}_{0}{b}^{2}}{ml(r+R){t}_{0}}$ 和方向垂直极板向左;
(3)电场力做的功为零,或$\frac{1}{2}ma{t}_{0}(a{t}_{0}-{v}_{0})$.
点评 考查电学与力学综合问题,掌握法拉第电磁感应定律、闭合电路欧姆定律、焦耳定律与楞次定律的应用,理解牛顿第二定律与运动学公式的运用,注意第3问中,分情况讨论是解题的重点,也是关键点.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案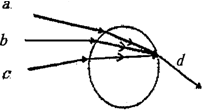
| A. | 在真空中,a光传播速度比b、c大 | |
| B. | b光的频率比c光小 | |
| C. | a光的光子能量最小 | |
| D. | 在玻璃砖中,a光传播速度比b、c小 | |
| E. | 若以a、b、c三种单色光分别用相同的装置做“用双缝干涉测定单色光的波长”的实验,则a光观察到的条纹间距最大 |
 如图,在光滑绝缘的倾角为30°的斜面内有平行斜面的水平匀强磁场,长为l的轻绳一端固定在O点另一端系一带电小球,使小球恰能在斜面内做圆周运动.已知其所受电场力等于重力的一半,小球质量为m,重力加速度为g.则( )
如图,在光滑绝缘的倾角为30°的斜面内有平行斜面的水平匀强磁场,长为l的轻绳一端固定在O点另一端系一带电小球,使小球恰能在斜面内做圆周运动.已知其所受电场力等于重力的一半,小球质量为m,重力加速度为g.则( )| A. | 小球的最小速率为$\sqrt{gl}$ | B. | 小球的最小速率为$\sqrt{\frac{gl}{2}}$ | ||
| C. | 绳中最大拉力为5.5mg | D. | 绳中最大拉力为3$\sqrt{2}$mg |
 如图所示为两列简谐横波在同一绳上传播时某时刻的波形图,质点M的平衡位置为x=0.2m.则下列说法中正确的是( )
如图所示为两列简谐横波在同一绳上传播时某时刻的波形图,质点M的平衡位置为x=0.2m.则下列说法中正确的是( )| A. | 这两列波发生干涉现象,且质点M的振动始终加强 | |
| B. | 由图示时刻开始,再经过$\frac{1}{4}$甲波周期,M将位于波峰 | |
| C. | 甲波的速度v1与乙波的速度v2一样大 | |
| D. | 因波的周期未知,故两列波波速的大小无法比较 |
| A. | 1 | B. | 10 | C. | 100 | D. | 1000 |
 卢瑟福通过α粒子散射实验,判断出原子中心有一个很小的核,并由此提出了原子的核式结构学说.如图所示的平面示意图中①、③两条线表示α粒子运动的轨迹,则沿③所示方向射向原子核的α粒子可能的运动轨迹是( )
卢瑟福通过α粒子散射实验,判断出原子中心有一个很小的核,并由此提出了原子的核式结构学说.如图所示的平面示意图中①、③两条线表示α粒子运动的轨迹,则沿③所示方向射向原子核的α粒子可能的运动轨迹是( )| A. | 轨迹a | B. | 轨迹b | C. | 轨迹c | D. | 轨迹d |
 2011年3月10日12时58分云南盈江发生了5.8级地震.在抗震救灾中,我国自主研制的“北斗一号“卫星导航系统,在抗震救灾中发挥了巨大作用.北斗导航系统又被称为“双星定位系统“,具有导航、定位等功能.“北斗“系统中两颗工作星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的AB两位置 (如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列判断中正确的是( )
2011年3月10日12时58分云南盈江发生了5.8级地震.在抗震救灾中,我国自主研制的“北斗一号“卫星导航系统,在抗震救灾中发挥了巨大作用.北斗导航系统又被称为“双星定位系统“,具有导航、定位等功能.“北斗“系统中两颗工作星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的AB两位置 (如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列判断中正确的是( )| A. | 这两颗卫星的加速度大小相等,均为$\frac{{R}^{2}g}{{r}^{2}}$ | |
| B. | 卫星1向后喷气就一定能追上卫星2 | |
| C. | 卫星1由位置A运动至位置B所需的时间为$\frac{πr}{R}$$\sqrt{\frac{r}{g}}$ | |
| D. | 卫星1由位置A运动到位置B的过程中万有引力做功为零 |
 如图所示,在x轴上方存在匀强磁场,磁感应强度为B,方向垂直纸面向里.在x轴下方存在匀强电场,方向竖直向上.一个质量为m,电荷量为q,重力不计的带正电粒子从y轴上的a(h,0)点沿y轴正方向以某一初速度开始运动,经过一段时间后,粒子与x轴正方向成45°进入电场,当粒子经过y轴的b点时速度方向恰好与y轴垂直.求:
如图所示,在x轴上方存在匀强磁场,磁感应强度为B,方向垂直纸面向里.在x轴下方存在匀强电场,方向竖直向上.一个质量为m,电荷量为q,重力不计的带正电粒子从y轴上的a(h,0)点沿y轴正方向以某一初速度开始运动,经过一段时间后,粒子与x轴正方向成45°进入电场,当粒子经过y轴的b点时速度方向恰好与y轴垂直.求: 如图所示,AB是与水平面成37°的绝缘光滑倾斜长直轨道,B点为长直轨道的底端,图中圆弧CD是半径为0.5m的半圆绝缘轨道,虚线CD为直径,两个轨道在同一竖直平面内,在分别过B、C两点的竖直虚线之间的空间内存在垂直纸面向里的匀强磁场,过B点的竖直虚线的右侧的整个空间存在水平向左的匀强电场,质量为0.20kg的可视为质点的带正电小球从直轨道上由静止开始沿斜面下滑,到达B点后离开直轨道,沿BC方向做匀速直线运动,并恰好沿着圆弧的切线方向进入半圆绝缘轨道运动,最后刚好能通过D点,已知小球在长直轨道上下滑的竖直高度h=3.20m,不计空气阻力,且小球带电量保持不变,g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,AB是与水平面成37°的绝缘光滑倾斜长直轨道,B点为长直轨道的底端,图中圆弧CD是半径为0.5m的半圆绝缘轨道,虚线CD为直径,两个轨道在同一竖直平面内,在分别过B、C两点的竖直虚线之间的空间内存在垂直纸面向里的匀强磁场,过B点的竖直虚线的右侧的整个空间存在水平向左的匀强电场,质量为0.20kg的可视为质点的带正电小球从直轨道上由静止开始沿斜面下滑,到达B点后离开直轨道,沿BC方向做匀速直线运动,并恰好沿着圆弧的切线方向进入半圆绝缘轨道运动,最后刚好能通过D点,已知小球在长直轨道上下滑的竖直高度h=3.20m,不计空气阻力,且小球带电量保持不变,g取10m/s2,sin37°=0.6,cos37°=0.8,求: