题目内容
15. 如图所示,在匀强磁场中匀速转动的单匝纯电阻矩形线圈的周期为T,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A.下列说法正确的是( )
如图所示,在匀强磁场中匀速转动的单匝纯电阻矩形线圈的周期为T,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A.下列说法正确的是( )| A. | 线圈消耗的电功率为1W | |
| B. | 线圈中感应电流的有效值为2A | |
| C. | 任意时刻线圈中的感应电动势为e=2$\sqrt{2}cos\frac{2π}{T}$t | |
| D. | 任意时刻穿过线圈的磁通量为φ=$\frac{2T}{π}sin\frac{2π}{T}$t |
分析 绕垂直于磁场方向的转轴在匀强磁场中匀速转动的矩形线圈中产生正弦或余弦式交流电,
由于从垂直中性面开始其瞬时表达式为i=Imcosθ,由已知可求Im=$\frac{i}{cosθ}$,
根据正弦式交变电流有效值和峰值关系可求电流有效值
根据P=I2R可求电功率
根据Em=Imr可求感应电动势的最大值
任意时刻穿过线圈的磁通量为Φ=$BSsin\frac{2π}{T}$ 根据Em=NBSω可求Φm=BS=$\frac{{E}_{m}}{NB}$
解答 解:A、从垂直中性面开始其瞬时表达式为i=Imcosθ,
则电流的最大值为:Im=$\frac{i}{cosθ}$=2A
线圈消耗的电功率为:P=I2r=$(\frac{\sqrt{2}}{2}{I}_{m})^{2}r$=4W,故A错误;
B、有效值为:I=$\frac{{I}_{m}}{\sqrt{2}}=\sqrt{2}A$,故B错误
C、感应电动势的最大值为:Em=Imr=2×2=4V
任意时刻线圈中的感应电动势为:e=Emcos$\frac{2π}{T}$=4cos$\frac{2π}{T}$t,故C错误;
D、任意时刻穿过线圈的磁通量为:Φ=$BSsin\frac{2π}{T}$t
根据公式Em=NBSω=NΦm$\frac{2π}{T}$可得:$\frac{{E}_{m}}{Nω}$=$\frac{2π}{π}$
故Φ=$\frac{2T}{π}sin\frac{2π}{T}t$,故D正确;
故选:D
点评 本题考查交流电的产生的及计算,要注意明确在计算中求解电功率及电表示数时要用有效值;求解电量时要用平均值.

练习册系列答案
相关题目
5. 如图所示,半径为2r的弹性螺旋线圈内有垂直于纸面向外的圆形匀强磁场区域,磁场区域的半径为r,磁感应强度为B,已知弹性螺旋线圈的电阻为R,线圈与磁场区域共圆心,则以下说法中正确的是( )
如图所示,半径为2r的弹性螺旋线圈内有垂直于纸面向外的圆形匀强磁场区域,磁场区域的半径为r,磁感应强度为B,已知弹性螺旋线圈的电阻为R,线圈与磁场区域共圆心,则以下说法中正确的是( )
 如图所示,半径为2r的弹性螺旋线圈内有垂直于纸面向外的圆形匀强磁场区域,磁场区域的半径为r,磁感应强度为B,已知弹性螺旋线圈的电阻为R,线圈与磁场区域共圆心,则以下说法中正确的是( )
如图所示,半径为2r的弹性螺旋线圈内有垂直于纸面向外的圆形匀强磁场区域,磁场区域的半径为r,磁感应强度为B,已知弹性螺旋线圈的电阻为R,线圈与磁场区域共圆心,则以下说法中正确的是( )| A. | 在线圈的半径由2r变到3r的过程中,线圈内有沿顺时针方向的电流 | |
| B. | 在线圈的半径由2r变到1.5r的过程中,线圈内有沿顺时针方向的电流 | |
| C. | 在线圈的半径由2r变到0.5r的过程中,通过线圈横截面上的电荷量为$\frac{3π{r}^{2}B}{4R}$ | |
| D. | 在线圈的半径由2r变到0.5r的过程中,通过线圈横截面上的电荷量为$\frac{15π{r}^{2}B}{4R}$ |
6. 如图所示,一束光线通过一水平界面从某介质射入真空,已知入射光线与界面的夹角为60°,折射光线与界面的夹角为45°,则该介质的折射率为( )
如图所示,一束光线通过一水平界面从某介质射入真空,已知入射光线与界面的夹角为60°,折射光线与界面的夹角为45°,则该介质的折射率为( )
 如图所示,一束光线通过一水平界面从某介质射入真空,已知入射光线与界面的夹角为60°,折射光线与界面的夹角为45°,则该介质的折射率为( )
如图所示,一束光线通过一水平界面从某介质射入真空,已知入射光线与界面的夹角为60°,折射光线与界面的夹角为45°,则该介质的折射率为( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
3.某同学利用如图(甲)所示的实验装置验证机械能守恒定律.实验所用电源为学生电源,输出电压为6V的交流电和直流电两种.图(乙)是他认为较理想的一条纸带,O点是打点计时器打出的第一个点(初速为零),A、B、C、D、E、F点是纸带上相邻的点.他们测出了各点与O点的距离h后做出了必要的计算,测量记录见下表

(1)距离h的记录中不符合有效数字读数的一组是A(填写计数点名称).
(2)下面列举了该实验的几个操作步骤:
A.按照图示的装置安装器件
B.将打点计时器接到电源的“直流输出”上;
C.用天平测出重锤的质量
D.释放纸带,立即接通电源开关打出一条纸带;
E.测量纸带上某些点间的距离;
F.根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能
其中没有必要进行的或者操作不当的步骤是BCD(填选项对应的字母);
(3)打点计时器的频率为50Hz,则计时器打下C点时,重物的速度大小为1.56m/s;
(4)计数点C、D、E与O点之间的距离分别用hC、hD、hE表示,打点计时器的打点周期用T表示,若重物质量为m,重力加速度为g,则从O到D重物动能的增加量△Ek=$\frac{m({h}_{E}-{h}_{C})^{2}}{8{T}^{2}}$;O到D重物重力势能的减少量△EP=mghD(△Ek、△EP均用hC、hD、hE、T、m、g符号表示).

| 计数点 | A | B | C | D | E | F |
| h/cm | 6.9 | 9.47 | 12.40 | 15.71 | 19.41 | 23.49[ |
(2)下面列举了该实验的几个操作步骤:
A.按照图示的装置安装器件
B.将打点计时器接到电源的“直流输出”上;
C.用天平测出重锤的质量
D.释放纸带,立即接通电源开关打出一条纸带;
E.测量纸带上某些点间的距离;
F.根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能
其中没有必要进行的或者操作不当的步骤是BCD(填选项对应的字母);
(3)打点计时器的频率为50Hz,则计时器打下C点时,重物的速度大小为1.56m/s;
(4)计数点C、D、E与O点之间的距离分别用hC、hD、hE表示,打点计时器的打点周期用T表示,若重物质量为m,重力加速度为g,则从O到D重物动能的增加量△Ek=$\frac{m({h}_{E}-{h}_{C})^{2}}{8{T}^{2}}$;O到D重物重力势能的减少量△EP=mghD(△Ek、△EP均用hC、hD、hE、T、m、g符号表示).
10. 如图所示,质量为m、长为L的导体棒MN电阻为R,起初静止于光滑的水平轨道上,电源电动势为E,内阻不计.匀强磁场的磁感应强度为B,其方向与轨道平面成θ角斜向上方,电键闭合后导体棒开始运动.下列说法不正确的是( )
如图所示,质量为m、长为L的导体棒MN电阻为R,起初静止于光滑的水平轨道上,电源电动势为E,内阻不计.匀强磁场的磁感应强度为B,其方向与轨道平面成θ角斜向上方,电键闭合后导体棒开始运动.下列说法不正确的是( )
 如图所示,质量为m、长为L的导体棒MN电阻为R,起初静止于光滑的水平轨道上,电源电动势为E,内阻不计.匀强磁场的磁感应强度为B,其方向与轨道平面成θ角斜向上方,电键闭合后导体棒开始运动.下列说法不正确的是( )
如图所示,质量为m、长为L的导体棒MN电阻为R,起初静止于光滑的水平轨道上,电源电动势为E,内阻不计.匀强磁场的磁感应强度为B,其方向与轨道平面成θ角斜向上方,电键闭合后导体棒开始运动.下列说法不正确的是( )| A. | 导体棒向右运动 | |
| B. | 电键闭合瞬间导体棒MN所受安培力为$\frac{BEL}{R}$ | |
| C. | 电键闭合瞬间导体棒MN所受安培力为$\frac{BELsinθ}{R}$ | |
| D. | 电键闭合瞬间导体棒MN的加速度为$\frac{BELsinθ}{mR}$ |
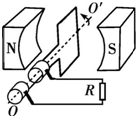 如图所示,一小型发电机内有N=100匝矩形线圈,线圈面积S=0.10m2,线圈总电阻r=1Ω.在外力作用下矩形线圈在磁感应强度B=0.10T的匀强磁场中,以恒定的转速n=50r/s绕垂直于磁场方向的固定轴OO'匀速转动,发电机线圈两端与R=9Ω的电阻构成闭合回路.从线圈平面通过中性面时开始计时.求:
如图所示,一小型发电机内有N=100匝矩形线圈,线圈面积S=0.10m2,线圈总电阻r=1Ω.在外力作用下矩形线圈在磁感应强度B=0.10T的匀强磁场中,以恒定的转速n=50r/s绕垂直于磁场方向的固定轴OO'匀速转动,发电机线圈两端与R=9Ω的电阻构成闭合回路.从线圈平面通过中性面时开始计时.求: 如图,太阳系中星体A绕太阳做半径为R1的圆周运动,星体B作抛物线运动,B在近日点处与太阳的相距为R2=2R1,且两轨道在同一平面上,两星体运动方向如图中箭头所示.设B运动到近日点时,A恰好运动到B与太阳连线上.A、B随即发生某种强烈的相互作用而迅速合并成一个新的星体,其间的质量损失可忽略,试证明新星体绕太阳的运动轨道为椭圆.
如图,太阳系中星体A绕太阳做半径为R1的圆周运动,星体B作抛物线运动,B在近日点处与太阳的相距为R2=2R1,且两轨道在同一平面上,两星体运动方向如图中箭头所示.设B运动到近日点时,A恰好运动到B与太阳连线上.A、B随即发生某种强烈的相互作用而迅速合并成一个新的星体,其间的质量损失可忽略,试证明新星体绕太阳的运动轨道为椭圆.