题目内容
13. 如图所示为圆弧形固定光滑轨道,a点切线方向与水平方向夹角53°,b点切线方向水平.一小球以水平初速度6m/s做平抛运动刚好能沿轨道切线方向进入轨道,已知轨道半径1m,小球质量1kg.(sin53=0.8,cos53=0.6,g=10m/s2)
如图所示为圆弧形固定光滑轨道,a点切线方向与水平方向夹角53°,b点切线方向水平.一小球以水平初速度6m/s做平抛运动刚好能沿轨道切线方向进入轨道,已知轨道半径1m,小球质量1kg.(sin53=0.8,cos53=0.6,g=10m/s2) (1)求小球做平抛运动的飞行时间;
(2)小球到达b点时,轨道对小球压力大小.
分析 (1)根据几何关系求出平抛运动到达a点时的竖直方向速度,进而求出平抛运动时间;
(2)根据平抛运动基本公式结合几何关系求解从抛出点到b的竖直高度,从初始位置到b,根据动能定理求出到达b点的速度,再在b点,根据牛顿第二定律求解即可.
解答 解:(1)进入轨道时速度方向与水平方向夹角为53°
有$\frac{{v}_{y}}{{v}_{0}}$=tan53°
Vy=gt
得t=0.8s,
(2)初始位置距a点高度h,
h=$\frac{1}{2}$gt2
h=3.2m
初始位置距b点高度H,
H=h-(R+$\frac{3}{5}$R)
H=1.6m
从初始位置到b,根据动能定理得:
mgH=$\frac{1}{2}$mvb2-$\frac{1}{2}$mv02
在b点,根据牛顿第二定律得
N+mg=m$\frac{{v}_{b}^{2}}{R}$
解得:N=58N
答:(1)小球做平抛运动的飞行时间为0.8s;
(2)小球到达b点时,轨道对小球压力大小为58N.
点评 本题结合平抛运动和圆周运动考查动能定理的应用,要求同学们能正确分析小球的运动情况,知道平抛运动水平方向做匀速直线运动,竖直方向做自由落体运动.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
3.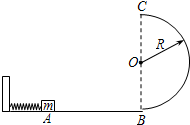 如图所示,竖直面内的半圆形轨道与光滑水平面在B点相切,半圆形轨道的半径为R,一个质量为m的物体将弹簧压缩至A点后静止释放,物体脱离弹簧时获得某一向右的速度,当它经过B点进入轨道的瞬间对轨道的压力为其中立的8倍,之后向上运动恰能达到最高点C,轨道上的D点于圆心O登高,不计空气阻力,则下列说法正确的是( )
如图所示,竖直面内的半圆形轨道与光滑水平面在B点相切,半圆形轨道的半径为R,一个质量为m的物体将弹簧压缩至A点后静止释放,物体脱离弹簧时获得某一向右的速度,当它经过B点进入轨道的瞬间对轨道的压力为其中立的8倍,之后向上运动恰能达到最高点C,轨道上的D点于圆心O登高,不计空气阻力,则下列说法正确的是( )
 如图所示,竖直面内的半圆形轨道与光滑水平面在B点相切,半圆形轨道的半径为R,一个质量为m的物体将弹簧压缩至A点后静止释放,物体脱离弹簧时获得某一向右的速度,当它经过B点进入轨道的瞬间对轨道的压力为其中立的8倍,之后向上运动恰能达到最高点C,轨道上的D点于圆心O登高,不计空气阻力,则下列说法正确的是( )
如图所示,竖直面内的半圆形轨道与光滑水平面在B点相切,半圆形轨道的半径为R,一个质量为m的物体将弹簧压缩至A点后静止释放,物体脱离弹簧时获得某一向右的速度,当它经过B点进入轨道的瞬间对轨道的压力为其中立的8倍,之后向上运动恰能达到最高点C,轨道上的D点于圆心O登高,不计空气阻力,则下列说法正确的是( )| A. | 物体在A点时弹簧的弹性势能为3mgR | |
| B. | 物体从B点运动至D点的过程中产生的内能为$\frac{1}{2}$mgR | |
| C. | 物体从B点运动至C点的过程中产生的内能为mgR | |
| D. | 物体从A点运动至C点的过程中机械能守恒 |
4. 长为l的轻绳,一端用质量为M的环固定在横杆上(轻绳质量不计),另一端连接一质量为m的小球,开始时,将系球的绳子绷紧并转到与横杆平行位置,然后轻轻放手,不计一切阻力.则( )
长为l的轻绳,一端用质量为M的环固定在横杆上(轻绳质量不计),另一端连接一质量为m的小球,开始时,将系球的绳子绷紧并转到与横杆平行位置,然后轻轻放手,不计一切阻力.则( )
 长为l的轻绳,一端用质量为M的环固定在横杆上(轻绳质量不计),另一端连接一质量为m的小球,开始时,将系球的绳子绷紧并转到与横杆平行位置,然后轻轻放手,不计一切阻力.则( )
长为l的轻绳,一端用质量为M的环固定在横杆上(轻绳质量不计),另一端连接一质量为m的小球,开始时,将系球的绳子绷紧并转到与横杆平行位置,然后轻轻放手,不计一切阻力.则( )| A. | 小球一直处于失重状态 | B. | 小球一直处于超重状态 | ||
| C. | 小球在最低点绳的拉力最大 | D. | 小球在最低点绳的拉力最小 |
8. 在水平桌面上有一个质量为M且倾角为α的斜面体.一个质量为m的物体,在平行于斜面的拉力F作用下,沿斜面向上做匀速运动.斜面体始终处于静止状态.已知物块与斜面间的动摩擦因数为μ,重力加速度为g.下列结论正确的是( )
在水平桌面上有一个质量为M且倾角为α的斜面体.一个质量为m的物体,在平行于斜面的拉力F作用下,沿斜面向上做匀速运动.斜面体始终处于静止状态.已知物块与斜面间的动摩擦因数为μ,重力加速度为g.下列结论正确的是( )
 在水平桌面上有一个质量为M且倾角为α的斜面体.一个质量为m的物体,在平行于斜面的拉力F作用下,沿斜面向上做匀速运动.斜面体始终处于静止状态.已知物块与斜面间的动摩擦因数为μ,重力加速度为g.下列结论正确的是( )
在水平桌面上有一个质量为M且倾角为α的斜面体.一个质量为m的物体,在平行于斜面的拉力F作用下,沿斜面向上做匀速运动.斜面体始终处于静止状态.已知物块与斜面间的动摩擦因数为μ,重力加速度为g.下列结论正确的是( )| A. | 斜面对物块的摩擦力大小是F | |
| B. | 斜面对物块的摩擦力大小是μmg | |
| C. | 桌面对斜面体的摩擦力大小是Fcosα | |
| D. | 桌面对斜面体的支持力大小是(M+m)g |
18.一个小球从楼顶以速度v0水平抛出,它落地速度为vt不计空气阻力,重力加速度g,则小球运动时间为( )
| A. | $\frac{{{v_t}+{v_0}}}{t}$ | B. | $\frac{{{v_t}-{v_0}}}{t}$ | C. | $\frac{{\sqrt{v_t^2-v_0^2}}}{g}$ | D. | $\frac{{\sqrt{v_t^2+v_0^2}}}{g}$ |
5. 如图所示,两个斜面体AC、BC,上端靠在同一竖直墙面上,下端交于水平面上同一点C,现让两个质量相同的物体分别从两个斜面的顶端同时由静止释放,则下列说法正确的是( )
如图所示,两个斜面体AC、BC,上端靠在同一竖直墙面上,下端交于水平面上同一点C,现让两个质量相同的物体分别从两个斜面的顶端同时由静止释放,则下列说法正确的是( )
 如图所示,两个斜面体AC、BC,上端靠在同一竖直墙面上,下端交于水平面上同一点C,现让两个质量相同的物体分别从两个斜面的顶端同时由静止释放,则下列说法正确的是( )
如图所示,两个斜面体AC、BC,上端靠在同一竖直墙面上,下端交于水平面上同一点C,现让两个质量相同的物体分别从两个斜面的顶端同时由静止释放,则下列说法正确的是( )| A. | 若两个斜面光滑,则沿BC下滑的物体一定先到达C点 | |
| B. | 若两个斜面光滑,则两个物体有可能同时到达C点 | |
| C. | 若两个斜面粗糙,且粗糙程度相同,则两个物体下滑到C点过程中损失的机械能一定相同 | |
| D. | 若两个斜面粗糙,且粗糙程度相同,则两个物体下滑到C点时的动能可能相同 |
2.一个小球做竖直上抛运动,与某一给定的位移对应的时刻( )
| A. | 只有一个 | B. | 可能有两个 | C. | 可能有三个 | D. | 可能有四个 |
3. 如图所示,水平圆盘上同一半径方向放着用长为r的细绳相连、可视为质点的A、B两物体,A、B的质量分别为2m、m,A到圆盘圆心的距离为r,两物体与圆盘的动摩擦因数相同,若圆盘从静止开始绕过圆心的竖直轴OO′缓慢地加速转动,当角速度增大到ω0时A开始滑动,同时细绳突然断裂,则细绳的最大张力为(取重力加速度为g)( )
如图所示,水平圆盘上同一半径方向放着用长为r的细绳相连、可视为质点的A、B两物体,A、B的质量分别为2m、m,A到圆盘圆心的距离为r,两物体与圆盘的动摩擦因数相同,若圆盘从静止开始绕过圆心的竖直轴OO′缓慢地加速转动,当角速度增大到ω0时A开始滑动,同时细绳突然断裂,则细绳的最大张力为(取重力加速度为g)( )
 如图所示,水平圆盘上同一半径方向放着用长为r的细绳相连、可视为质点的A、B两物体,A、B的质量分别为2m、m,A到圆盘圆心的距离为r,两物体与圆盘的动摩擦因数相同,若圆盘从静止开始绕过圆心的竖直轴OO′缓慢地加速转动,当角速度增大到ω0时A开始滑动,同时细绳突然断裂,则细绳的最大张力为(取重力加速度为g)( )
如图所示,水平圆盘上同一半径方向放着用长为r的细绳相连、可视为质点的A、B两物体,A、B的质量分别为2m、m,A到圆盘圆心的距离为r,两物体与圆盘的动摩擦因数相同,若圆盘从静止开始绕过圆心的竖直轴OO′缓慢地加速转动,当角速度增大到ω0时A开始滑动,同时细绳突然断裂,则细绳的最大张力为(取重力加速度为g)( )| A. | $\frac{1}{2}$mω02r | B. | $\frac{2}{3}$mω02r | C. | $\frac{3}{2}$mω02r | D. | $\frac{4}{3}$mω02r |
 重庆某中学物理兴趣小组决定举行遥控赛车比赛,比赛路径如图所示.可视为质点的赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直半圆轨道,并通过半圆轨道的最高点C,才算完成比赛.B是半圆轨道的最低点,水平直线轨道和半圆轨道相切于B点.已知赛车质量m=0.5kg,通电后以额定功率P=2W工作,进入竖直圆轨道前受到的阻力恒为Ff=0.4N,随后在运动中受到的阻力均可不计,L=10.00m,R=0.4m,(g取10m/s2).求:
重庆某中学物理兴趣小组决定举行遥控赛车比赛,比赛路径如图所示.可视为质点的赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直半圆轨道,并通过半圆轨道的最高点C,才算完成比赛.B是半圆轨道的最低点,水平直线轨道和半圆轨道相切于B点.已知赛车质量m=0.5kg,通电后以额定功率P=2W工作,进入竖直圆轨道前受到的阻力恒为Ff=0.4N,随后在运动中受到的阻力均可不计,L=10.00m,R=0.4m,(g取10m/s2).求: