题目内容
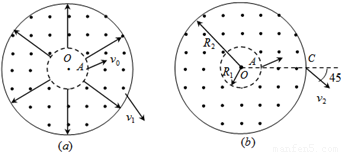
如图（a）所示，在以O为圆心，内外半径分别为R1和R2的圆环区域内，存在辐射状电场和垂直纸面的匀强磁场，内外圆间的电势差U为常量，R1=R，R2=3R，一电荷量为+q，质量为m的粒子从内圆上的A点进入该区域，不计重力．（1）已知粒子从外圆上以速度v1射出，求粒子在A点的初速度v的大小；
（2）若撤去电场，如图（b），已知粒子从OA延长线与外圆的交点C以速度v2射出，方向与OA延长线成45°角，求磁感应强度的大小及粒子在磁场中运动的时间；
（3）在图（b）中，若粒子从A点进入磁场，速度大小为v3，方向不确定，要使粒子一定能够从外圆射出，磁感应强度应小于多少？
【答案】分析：带电粒子在电场与磁场中，只有电场力对粒子做功，所以由动能定理可求出初速度．由于粒子从OA延长线与外圆的交点C以速度v2射出，则入射点与出射点连续是弦，因此弦的中垂线与射出速度的垂线交点即为轨道的圆心．从而由几何关系可求出磁感应强度大小及运动的时间．若粒子从A点进入磁场，速度大小一定，方向不定，要使粒子一定能够从外圆射出，粒子在磁场内的运动半径应大于过A点的最大内切圆半径，所以由轨道半径从而求出最小磁感应强度．
解答：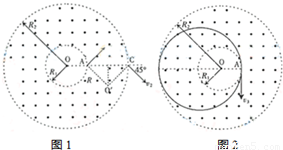
解：（1）电、磁场都存在时，只有电场力对带电粒子做功，由动能定理
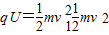①
得
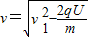②
（2）由牛顿第二定律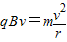
③
如图1，由几何关系粒子运动轨迹的圆心O′和半径R
则有：R2+R2=（R2-R1）2④
联立③④得磁感应强度大小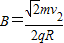
⑤
粒子在磁场中做匀速圆周运动的周期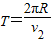
⑥
由几何关系确定粒子在磁场中运动的时间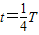
⑦
由④⑥⑦式，得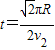
⑧
（3）如图2，为使粒子射出，则粒子在磁场内的运动半径应大于过A点的最大内切圆半径，该半径为
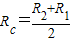⑨
由③⑨，得磁感应强度应小于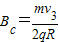
点评：解决粒子做匀速圆周运动的步骤：定圆心、画圆弧、求半径．同时若粒子从A点进入磁场，速度大小一定而方向不定，要使粒子一定能够从外圆射出，求磁感应强度应最大值，则粒子在磁场内的运动半径应大于过A点的最小内切圆半径．
解答：
解：（1）电、磁场都存在时，只有电场力对带电粒子做功，由动能定理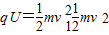①得
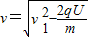②（2）由牛顿第二定律
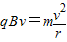③如图1，由几何关系粒子运动轨迹的圆心O′和半径R
则有：R2+R2=（R2-R1）2④
联立③④得磁感应强度大小
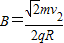⑤粒子在磁场中做匀速圆周运动的周期
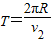⑥由几何关系确定粒子在磁场中运动的时间
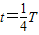⑦由④⑥⑦式，得
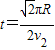⑧（3）如图2，为使粒子射出，则粒子在磁场内的运动半径应大于过A点的最大内切圆半径，该半径为
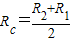⑨由③⑨，得磁感应强度应小于
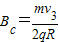
点评：解决粒子做匀速圆周运动的步骤：定圆心、画圆弧、求半径．同时若粒子从A点进入磁场，速度大小一定而方向不定，要使粒子一定能够从外圆射出，求磁感应强度应最大值，则粒子在磁场内的运动半径应大于过A点的最小内切圆半径．
练习册系列答案
相关题目
（2011?广东）如图（a）所示，在以O为圆心，内外半径分别为R1和R2的圆环区域内，存在辐射状电场和垂直纸面的匀强磁场，内外圆间的电势差U为常量，R1=R0，R2=3R0，一电荷量为+q，质量为m的粒子从内圆上的A点进入该区域，不计重力．
．（要求画出粒子在磁场中运动轨迹的示意图）
．（要求画出粒子在磁场中运动轨迹的示意图）
