Question

排球场总长18m，设球网高度为2m，运动员站在离网3m的线上正对网前跳起将球水平击出．（球飞行中阻力不计）
（1）设击球点在3m线正上方高度为2.5m，试问击球的速度在什么范围内才能使球既不触网也不出界；
（2）若击球点在3m线正上方的高度小于某个值，那么无论水平击球的速度多大，球不是触网就是越界，试求这个高度．（g=10m/s²）

Answer 1

分析：（1）排球飞出后做平抛运动，则由竖直高度可确定时间，则由水平位移可求得排球的速度范围；
（2）由题意可知满足条件的临界值，则由平抛运动的规律可得正确结果．

解答：解：
（1）排球被水平击出后，作平抛运动，作出如图所示的示意图．若正好压在底线上，则球在空中飞行的时间为t1=

2h0 g

=

2

2

s，
由此得排球越界的临界击球速度值为v1=

x1

t1

=12

2

m/s，
若球恰好触网，则球在球网上方运动的时间为t2=

2(h0-H) g

=

10

10

s，
由此求得排球触网的临界击球速度v2=x2/t2=3

10

m/s，
要使排球既不触网又不越界，水平击球速度v的取值范围为3

10

m/s＜v＜12

2

m/s．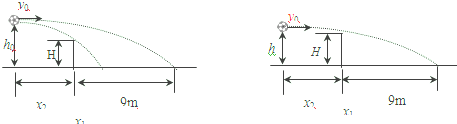
（2）设击球点的高度为h．当h较小时，击球速度过大会出界，击球速度过小又会触网，情况是球刚好擦网而过，落地时又恰压底线上（如图所示），
则有：

x1

2h g

=

x2

2(h-H) g

得h=2.13m，
即击球高度不超过此值时，球不是出界就是触网．

点评：本题考查平抛运动在生活中应用，要通过分析找出临界条件，由平抛运动的规律即可求解．