题目内容

精英家教网沿半径为R=0.5m的半球型碗底的光滑内表面，一个小球在水平面内作匀速圆周运动，小球距碗底的高度h=0.25m，试求小球做匀速圆周运动的角速度？（g取10m/s2）
分析：小球在光滑碗内靠重力和支持力的合力提供向心力，根据平行四边形定则求出合力的大小，结合牛顿第二定律求出小球做匀速圆周运动的角速度．
解答：解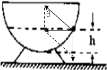：精英家教网小球靠重力和支持力的合力提供向心力，小球做圆周运动的半径为r=Rsinθ，根据力图可知小球的合力F合=mgtanθ．
根据几何关系知，cosθ=
0.25
0.5
=
1
2
，则θ=60°
则mgtanθ=mrω2，
解得：ω=
g
Rcosθ
=
10
0.5×
1
2
=2
10
rad/s．
答：小球做匀速圆周运动的角速度为2
10
rad/s．
点评：解决本题的关键知道小球做圆周运动向心力的来源，运用牛顿第二定律和几何关系进行求解．
练习册系列答案
相关题目
如图是半径为R=0.5m的光滑圆弧形轨道，直径AC水平，直径CD竖直．今有质量为m=1kg的小球a从A处以初速度v0=3
6
m/s沿圆弧运动，与静止在圆弧底端B处直径相同的小球b发生碰撞．则（g=10m/s2）
（1）小球a在A处对轨道的压力多大？（结果保留两位有效数字）
（2）若小球b质量也为m，且a、b发生弹性碰撞，则碰后小球b的速度多大？
（3）若小球b质量为km（k＞0），且a、b碰后粘在一起，欲使ab不脱离轨道求k的取值范围．
如图所示，水平桌面上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点．水平桌面右侧某一位置有一竖直放置的、左上角有一开口的光滑圆弧轨道MNP，其半径为R=0.5m，∠PON=53°，MN为其竖直直径，P点到桌面的竖直距离是h=0.8m．如用质量m1=0.4kg的物块将弹簧缓慢压缩到C点，释放后物块恰停止在桌面边缘D点．现换用同种材料制成的质量为m2=0.2kg的物块将弹簧缓慢压缩到C点，释放后物块能飞离桌面并恰好由P点沿切线滑入光滑圆轨道MNP（g取10m/s2，sin53°=0.8，cos53°=0.6）．
（1）求物体m2运动到M点时受到轨道的压力；
（2）求弹簧的弹性势能EP；
（3）如圆弧轨道的位置以及∠PON可任意调节，使从C点释放又从D点滑出的质量为m=km1物块都能由P点沿切线滑入圆弧轨道，并且还能通过最高点M，求k的取值范围．
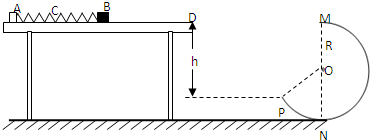
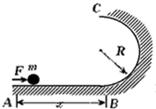如图所示，光滑水平面右端B处连接一个竖直的半径为R=0.5m的光滑半圆轨道．在距离B为x的A点，用水平恒定推力F=20N将质量为m=2kg的小球从静止开始推到B处后撤去水平推力，质点沿半圆轨道运动到最高点C处后又正好落回A点．则：
（1）小球到底C点时对轨道的压力为多少？
（2）距离x的值应为多少？（ g=10m/s2）
精英家教网如图所示，粗糙水平地面与半径为R=0.5m的光滑半圆轨道BCD相连接，且在同一竖直平面内，O是BCD的圆心，BOD在同一竖直线上．质量为m=1kg的小物块在水平恒力F=15N的作用下，由静止开始从A点开始做匀加速直线运动，当小物块运动到B点时撤去F，小物块沿半圆轨道运动恰好能通过D点，已知AB间的距离为3m，重力加速度g=10m/s2．求：
（1）小物块运动到B点时的速度；
（2）小物块离开D点后落到地面上的点与B点之间的距离；
（3）小物块在水平面上从A运动到B的过程中克服摩擦力做的功．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网