题目内容
如图所示,Ⅰ、Ⅱ区域是宽度均为L=0.5m的匀强磁场,磁感应强度大小B=1T,方向相反.一边长L=0.5m、质量m=0.1kg、电阻R=0.5Ω的正方形金属线框,在外力作用下,以初速度v=10m/s匀速穿过磁场区域.(1)取逆时针方向为正,作出i-t图象;
(2)求线框穿过磁场区域的过程中外力做的功;
(3)若不施加外力,确定线框最终停止的位置.
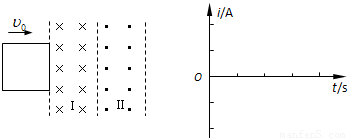
【答案】分析:(1)将线框穿过磁场的过程分成三段,分别根据感应电动势公式求出感应电动势,由右手定则判断感应电流方向.作出i-t图象.
(2)线框匀速穿过磁场区域时,外力做功等于线框中产生的焦耳热.
(3)若不施加外力,线框进入磁场后受到安培力,根据牛顿第二定律列出加速度表达式,将a=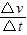 代入,并求和,采用积分法求出线框通过Ⅰ的过程线框的末速度,再对线框进入Ⅱ的过程,运用积分法求解线框进入磁场后运动的位移大小.
代入,并求和,采用积分法求出线框通过Ⅰ的过程线框的末速度,再对线框进入Ⅱ的过程,运用积分法求解线框进入磁场后运动的位移大小.
解答: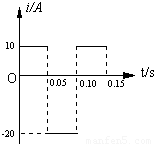 解:
解:
(1)感应电流I1=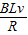 =10A,逆时针方向取正值;时间间隔t1=0.05s
=10A,逆时针方向取正值;时间间隔t1=0.05s
I2=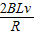 =20A,顺时针方向取负值;时间间隔t2=0.05s
=20A,顺时针方向取负值;时间间隔t2=0.05s
I3= =10A,逆时针方向取正值;时间间隔t3=0.05s
=10A,逆时针方向取正值;时间间隔t3=0.05s
电流随时间变化关系如图所示.
(2)因为线框匀速运动,所以外力做的功等于电流做的功
W= +
+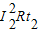 +
+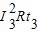 =15J
=15J
(3)没有外力时,线框在安培力作用下做变减速运动
线框通过Ⅰ的过程中:-
即-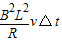 =m△v
=m△v
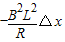 =m△v
=m△v
得到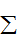
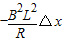 =
=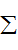 m△v
m△v
解得,v1=7.5m/s
线框进入Ⅱ的过程中:-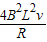 =ma=m
=ma=m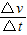
即-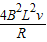 △t=m△v
△t=m△v
-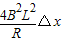 =m△v
=m△v
解得,x2=0.375m
即线框进入磁场后运动x=x1+x2=0.875m.
答:
(1)取逆时针方向为正,作出i-t图象如图;
(2)线框穿过磁场区域的过程中外力做的功为15J;
(3)若不施加外力,线框进入磁场后运动0.875m停止.
点评:本题难点是运用积分法求解非匀变速运动的速度和位移,关键从牛顿第二定律入手,根据加速度的定义式a=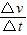 分析.
分析.
(2)线框匀速穿过磁场区域时,外力做功等于线框中产生的焦耳热.
(3)若不施加外力,线框进入磁场后受到安培力,根据牛顿第二定律列出加速度表达式,将a=
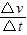 代入,并求和,采用积分法求出线框通过Ⅰ的过程线框的末速度,再对线框进入Ⅱ的过程,运用积分法求解线框进入磁场后运动的位移大小.
代入,并求和,采用积分法求出线框通过Ⅰ的过程线框的末速度,再对线框进入Ⅱ的过程,运用积分法求解线框进入磁场后运动的位移大小.解答:
 解:
解:(1)感应电流I1=
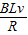 =10A,逆时针方向取正值;时间间隔t1=0.05s
=10A,逆时针方向取正值;时间间隔t1=0.05sI2=
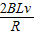 =20A,顺时针方向取负值;时间间隔t2=0.05s
=20A,顺时针方向取负值;时间间隔t2=0.05sI3=
 =10A,逆时针方向取正值;时间间隔t3=0.05s
=10A,逆时针方向取正值;时间间隔t3=0.05s电流随时间变化关系如图所示.
(2)因为线框匀速运动,所以外力做的功等于电流做的功
W=
 +
+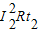 +
+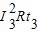 =15J
=15J(3)没有外力时,线框在安培力作用下做变减速运动
线框通过Ⅰ的过程中:-

即-
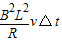 =m△v
=m△v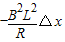 =m△v
=m△v得到
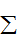
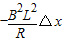 =
=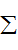 m△v
m△v解得,v1=7.5m/s
线框进入Ⅱ的过程中:-
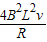 =ma=m
=ma=m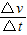
即-
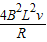 △t=m△v
△t=m△v-
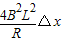 =m△v
=m△v解得,x2=0.375m
即线框进入磁场后运动x=x1+x2=0.875m.
答:
(1)取逆时针方向为正,作出i-t图象如图;
(2)线框穿过磁场区域的过程中外力做的功为15J;
(3)若不施加外力,线框进入磁场后运动0.875m停止.
点评:本题难点是运用积分法求解非匀变速运动的速度和位移,关键从牛顿第二定律入手,根据加速度的定义式a=
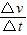 分析.
分析. 
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图所示,在圆形区域内有方向垂直向里的匀强磁场.有一束速率各不相同的质子自A点沿半径方向射入磁场,这些质子在磁场中( )
如图所示,在圆形区域内有方向垂直向里的匀强磁场.有一束速率各不相同的质子自A点沿半径方向射入磁场,这些质子在磁场中( )| A、速度越大的,运动时间越长 | B、运动时间越长的,其轨迹越长 | C、速度越大的,速度的偏转角越小 | D、所有质子在磁场中的运动时间相同 |
 (2012?河北模拟)如图所示装置中,区域Ⅰ和Ⅲ中分别有竖直向上和水平向右的匀强电场,电场强度分别为E和
(2012?河北模拟)如图所示装置中,区域Ⅰ和Ⅲ中分别有竖直向上和水平向右的匀强电场,电场强度分别为E和 (2011?宁德模拟)如图所示,在圆形区域内,存在垂直纸面向外的匀强磁场,ab是圆的一条直径.一带电粒子从a点射入磁场,速度大小为2v,方向与ab成30°时恰好从b点飞出磁场,粒子在磁场中运动的时间为t;若仅将速度大小改为v,则粒子在磁场中运动的时间为(不计带电粒子所受重力)( )
(2011?宁德模拟)如图所示,在圆形区域内,存在垂直纸面向外的匀强磁场,ab是圆的一条直径.一带电粒子从a点射入磁场,速度大小为2v,方向与ab成30°时恰好从b点飞出磁场,粒子在磁场中运动的时间为t;若仅将速度大小改为v,则粒子在磁场中运动的时间为(不计带电粒子所受重力)( ) 如图所示,在正方形区域abcd内有一垂直纸面向里的匀强磁场,一束电子自P点垂直于ad边射入磁场区域,下列判断正确的是( )
如图所示,在正方形区域abcd内有一垂直纸面向里的匀强磁场,一束电子自P点垂直于ad边射入磁场区域,下列判断正确的是( ) 如图所示,某空间区域分布着水平向里的匀强磁场,磁场区域的水平宽度d=0.4m,磁感应强度B=0.5T. 固定在绝缘平板上的竖直正方形金线框PQMN边长L=0.4m,电阻R=0.1Ω,整个属装置质量M=0.3kg,平板与水平面间的动摩擦因数为μ=0.2,用细线通过光滑定滑轮与质量为m=0.1kg的重物相连.现将重物由静止释放,使金属框向右运动,PQ边刚进入磁场时线框恰好做匀速运动.(最大静摩擦力等于滑动摩擦力)(g取10m/s2)求:
如图所示,某空间区域分布着水平向里的匀强磁场,磁场区域的水平宽度d=0.4m,磁感应强度B=0.5T. 固定在绝缘平板上的竖直正方形金线框PQMN边长L=0.4m,电阻R=0.1Ω,整个属装置质量M=0.3kg,平板与水平面间的动摩擦因数为μ=0.2,用细线通过光滑定滑轮与质量为m=0.1kg的重物相连.现将重物由静止释放,使金属框向右运动,PQ边刚进入磁场时线框恰好做匀速运动.(最大静摩擦力等于滑动摩擦力)(g取10m/s2)求: