题目内容
一质量为m、半径为r，电阻为R的金属圆环，竖直自由下落，经过一个磁感应强度为B的匀强磁场，当圆环进入磁场区域的竖直高度为d时，圆环所受的合外力为零，此时圆环的速度大小为| mgR |
| 4B2(2r-d)d |
| mgR |
| 4B2(2r-d)d |
分析：当圆环进入磁场区域时，圆环中产生感应电流，受到向上的安培力作用．根据法拉第电磁感应定律求出感应电动势，由欧姆定律求出感应电流，再求出安培力表达式，联立求解速度．
解答：解：当圆环进入磁场区域的竖直高度为d时，有效的切割长度为L=2
=2
圆环中产生的感应电动势为E=BLv，
感应电流为I=
圆环受到的安培力大小为F=BIL
联立得到F=
由题，圆环所受的合外力为零，则有F=mg
得到到
=mg
所以速度v=
=
．
故答案为：
| r2-(r-d)2 |
| 2rd-d2 |
圆环中产生的感应电动势为E=BLv，
感应电流为I=
| E |
| R |
圆环受到的安培力大小为F=BIL
联立得到F=
| B2L2v |
| R |
由题，圆环所受的合外力为零，则有F=mg
得到到
| B2L2v |
| R |
所以速度v=
| mgR |
| B2L2 |
| mgR |
| 4B2(2r-d)d |
故答案为：
| mgR |
| 4B2(2r-d)d |
点评：本题难点是确定圆环有效的切线长度．圆环产生的感应电动势相当于弦这么长的导线切线磁感线产生的．
练习册系列答案
相关题目
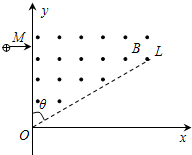如图所示，虚线OL与y轴的夹角为θ=60°，在此角范围内有垂直于xOy平面向外的匀强磁场，磁感应强度大小为B．一质量为m、电荷量为q（q＞0）的粒子从左侧平行于x轴射入磁场，入射点为M．粒子在磁场中运动的轨道半径为R．粒子离开磁场后的运动轨迹与x轴交于P点（图中未画出），且
如图所示，在距一质量为M、半径为R、密度均匀的球体R处有一质量为m的质点，此时球体对质点的万有引力为F1，当从球体中挖去一半径为
如图，一质量为m，半径为r的球，被长为r的细绳挂在光滑的竖直墙壁上，下列判断正确的是（ ）