题目内容
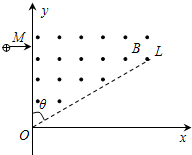 如图所示,虚线OL与y轴的夹角为θ=60°,在此角范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q(q>0)的粒子从左侧平行于x轴射入磁场,入射点为M.粒子在磁场中运动的轨道半径为R.粒子离开磁场后的运动轨迹与x轴交于P点(图中未画出),且
如图所示,虚线OL与y轴的夹角为θ=60°,在此角范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q(q>0)的粒子从左侧平行于x轴射入磁场,入射点为M.粒子在磁场中运动的轨道半径为R.粒子离开磁场后的运动轨迹与x轴交于P点(图中未画出),且. | OD |
分析:粒子进入磁场后做匀速圆周运动,找圆心,画出轨迹;离开磁场后沿出磁场方向做匀速直线运动.
解答: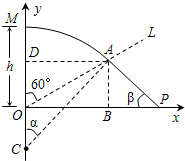 解:根据题意,粒子进入磁场后做匀速圆周运动,设运动轨迹交虚线OL于A点,圆心在y轴上的C点,AC与y轴的夹角为α;粒子从A点射出后,运动轨迹交x轴的P点,设AP与x轴的夹角为β,如右图所示
解:根据题意,粒子进入磁场后做匀速圆周运动,设运动轨迹交虚线OL于A点,圆心在y轴上的C点,AC与y轴的夹角为α;粒子从A点射出后,运动轨迹交x轴的P点,设AP与x轴的夹角为β,如右图所示
由牛顿第二定律得:qvB=m
①
周期为T=
=
②
过A点作x、y轴的垂线,垂足分别为B、D.
由几何知识得
=Rsinα,
=
cot60°,
=
cotβ,
=
+
,α=β ③
联立得到 sinα+
cosα=1
解得 α=30°,或α=90°
设M点到O点的距离为h,有
=Rsinα h=R-
,
=
-
=Rcosα-
联立得到 h=R-
Rcos(α+30°)(1分)
解得 h=(1-
)R(α=30°) 或 h=(1+
)R(α=90°)
当α=30°时,粒子在磁场中运动的时间为t=
=
当α=90°时,粒子在磁场中运动的时间为t=
=
答:M点到O点的距离h=(1-
)R或h=(1+
)R;粒子在磁场中运动的时间为
或
.
 解:根据题意,粒子进入磁场后做匀速圆周运动,设运动轨迹交虚线OL于A点,圆心在y轴上的C点,AC与y轴的夹角为α;粒子从A点射出后,运动轨迹交x轴的P点,设AP与x轴的夹角为β,如右图所示
解:根据题意,粒子进入磁场后做匀速圆周运动,设运动轨迹交虚线OL于A点,圆心在y轴上的C点,AC与y轴的夹角为α;粒子从A点射出后,运动轨迹交x轴的P点,设AP与x轴的夹角为β,如右图所示由牛顿第二定律得:qvB=m
| v2 |
| R |
周期为T=
| 2πR |
| v |
| 2πm |
| qB |
过A点作x、y轴的垂线,垂足分别为B、D.
由几何知识得
. |
| AD |
. |
| OD |
. |
| AD |
. |
| BP |
. |
| OD |
. |
| OP |
. |
| AD |
. |
| BP |
联立得到 sinα+
| 1 | ||
|
解得 α=30°,或α=90°
设M点到O点的距离为h,有
. |
| AD |
. |
| OC |
. |
| OC |
. |
| CD |
. |
| OD |
| ||
| 3 |
. |
| AD |
联立得到 h=R-
| 2 | ||
|
解得 h=(1-
| ||
| 3 |
| ||
| 3 |
当α=30°时,粒子在磁场中运动的时间为t=
| T |
| 12 |
| πm |
| 6qB |
当α=90°时,粒子在磁场中运动的时间为t=
| T |
| 4 |
| πm |
| 2qB |
答:M点到O点的距离h=(1-
| ||
| 3 |
| ||
| 3 |
| πm |
| 6qB |
| πm |
| 2qB |
点评:根据几何关系求出带电粒子在磁场中的偏转角有两个,要注意分别进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

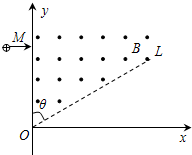
 =R.不计重力.求M点到O点的距离和粒子在磁场中运动的时间.
=R.不计重力.求M点到O点的距离和粒子在磁场中运动的时间.