题目内容
20. 某物体的位移-时间图象如下图所示,若规定向东为位移的正方向,试求:
某物体的位移-时间图象如下图所示,若规定向东为位移的正方向,试求:(1)物体在OA、AB、BC、CD、DE各阶段的速度;
(2)6s内和12s内的平均速度;
(3)物体在OA、AB、BC、CD、DE各阶段的加速度是多少.
分析 (1)位移-时间图线的斜率等于速度.根据数学知识求解.
(2)图象是物体通过的位移等于纵坐标的变化量.平均速度等于位移与时间的比值
(3)分析物体的运动情况,求解加速度.
解答 解:(1)根据位移-时间图线的斜率等于速度,可得OA,AB,BC、CD、DE各阶段的速度分别为:
v1=$\frac{6}{2}$m/s=3m/s,
v2=0,
v3=$\frac{12-6}{1}m/s=6m/s$
${v}_{4}=\frac{0-12}{2}m/s=-6m/s$
${v}_{5}=\frac{-4-0}{4}$m/s=-1m/s
(2)物体在6s内的位移为x6=12m
平均速度$\overline{v}=\frac{{x}_{6}}{{t}_{6}}=\frac{12}{6}m/s=2m/s$
物体在12s内的位移为:x12=-4-0=-4m
平均速度为$\overline{v′}=\frac{{x}_{12}}{{t}_{12}}=\frac{-4}{12}m/s=-\frac{1}{3}m/s$
(3)根据(1)可知,物体匀速运动,故加速度为0
答:(1)物体在OA、AB、BC、CD、DE各阶段的速度分别为3m/s,0,6m/s,-6m/s,-1m/s;
(2)6s内和12s内的平均速度分别为2m/s和-1m/s;
(3)物体在OA、AB、BC、CD、DE各阶段的加速度是都是0
点评 理解位移图象的斜率等于物体运动的速度,是我们解决此类问题的理论根据.

练习册系列答案
相关题目
8.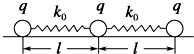 如图所示,在光滑绝缘水平面上放置3个相同的带电小球,小球之间用劲度系数均为k0,原长均为L的轻质弹簧绝缘连接.当3个小球处在静止状态时,每根弹簧的长度为l.已知静电力常量为k,若不考虑弹簧的静电感应,且假设小球的电荷量均为q(q>0),则每个小球的电荷量q为( )
如图所示,在光滑绝缘水平面上放置3个相同的带电小球,小球之间用劲度系数均为k0,原长均为L的轻质弹簧绝缘连接.当3个小球处在静止状态时,每根弹簧的长度为l.已知静电力常量为k,若不考虑弹簧的静电感应,且假设小球的电荷量均为q(q>0),则每个小球的电荷量q为( )
 如图所示,在光滑绝缘水平面上放置3个相同的带电小球,小球之间用劲度系数均为k0,原长均为L的轻质弹簧绝缘连接.当3个小球处在静止状态时,每根弹簧的长度为l.已知静电力常量为k,若不考虑弹簧的静电感应,且假设小球的电荷量均为q(q>0),则每个小球的电荷量q为( )
如图所示,在光滑绝缘水平面上放置3个相同的带电小球,小球之间用劲度系数均为k0,原长均为L的轻质弹簧绝缘连接.当3个小球处在静止状态时,每根弹簧的长度为l.已知静电力常量为k,若不考虑弹簧的静电感应,且假设小球的电荷量均为q(q>0),则每个小球的电荷量q为( )| A. | $\frac{4{k}_{0}{l}^{2}(L-l)}{5k}$ | B. | $\sqrt{\frac{4k{l}^{2}(l-L)}{5{k}_{0}}}$ | C. | $\sqrt{\frac{4k{l}^{2}(L-l)}{5k}}$ | D. | $\sqrt{\frac{4{k}_{0}{l}^{2}(l-L)}{5k}}$ |
9.在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图所示,在纸带上选择0、1、2、3、4、5的6个计数点,相邻两计数点之间还有四个点未画出,它们每相邻两个计数点之间的时间记为△t.纸带旁并排放着带有最小分度为毫米的刻度尺,零点跟“0”计数点对齐,由图可以读出三个计数点1、3、5跟0点的距离x1、x3、x5分别填入下列表格中.
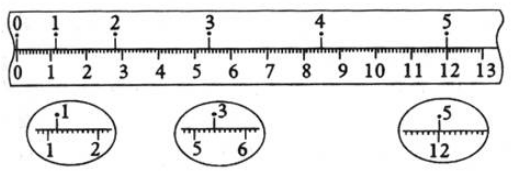
若取计数点“3”到“5”之间的平均速度为计数点“4”的瞬时速度,则小车通过计数点“4”的瞬时速度的表达式V4=$\frac{{x}_{5}-{x}_{3}}{2△t}$,代入数据可算得V4=0.33m/s;用同样的方法可算出得V2=0.21m/s;由加速度的计算公式可以得到小车从计数点“2”到计数点“4”的平均加速度表达式a=$\frac{{v}_{4}-{v}_{2}}{2△t}$,代入数据可计算得a=0.6m/s2.

| 距离 | x1 | x3 | x5 |
| 测量值/cm | 1.20 | 5.40 | 12.00 |
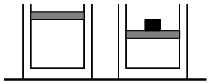 如图所示,容器放置于水平地面上,内部密封一定质量的理想气体.底面积为S、质量为m0的活塞可以沿容器壁无摩擦地自由滑动.大气压强为p0,容器导热良好,重力加速度为g,大气温度不变.初始系统平衡时,活塞与容器底部的高度差为h1.现将一个质量为m的小物块无初速地放在活塞上,当系统再次达到平衡时,活塞相对初始位置下降了多少?
如图所示,容器放置于水平地面上,内部密封一定质量的理想气体.底面积为S、质量为m0的活塞可以沿容器壁无摩擦地自由滑动.大气压强为p0,容器导热良好,重力加速度为g,大气温度不变.初始系统平衡时,活塞与容器底部的高度差为h1.现将一个质量为m的小物块无初速地放在活塞上,当系统再次达到平衡时,活塞相对初始位置下降了多少? 物体沿直线运动的v-t关系如图所示,已知在第1秒内合外力对物体做的功为W,则第1秒末到第3秒末合外力做功为0,第3秒末到第5秒末合外力的功为-W.
物体沿直线运动的v-t关系如图所示,已知在第1秒内合外力对物体做的功为W,则第1秒末到第3秒末合外力做功为0,第3秒末到第5秒末合外力的功为-W. 如图所示,是某质点运动的v-t图象,请回答:
如图所示,是某质点运动的v-t图象,请回答:
 物块A放在台秤上,通过跨过定滑轮的轻绳与物块B相连,B下端与一轻质弹簧粘连,弹簧的下端与地面接触(未栓接),整个系统处于静止状态,此时台秤示数为8.8N.已知mA=2mB=1kg,物块A、B间的水平距离s=20cm,倾斜绳与水平方向夹角θ0=37°,物块A与台秤间动摩擦因素μ=0.5,设最大静摩擦力等于滑动摩擦力.A、B和滑轮视为质点,不计滑轮质量和滑轮处摩擦,弹簧一直在弹性限度内,g取10m/s2.
物块A放在台秤上,通过跨过定滑轮的轻绳与物块B相连,B下端与一轻质弹簧粘连,弹簧的下端与地面接触(未栓接),整个系统处于静止状态,此时台秤示数为8.8N.已知mA=2mB=1kg,物块A、B间的水平距离s=20cm,倾斜绳与水平方向夹角θ0=37°,物块A与台秤间动摩擦因素μ=0.5,设最大静摩擦力等于滑动摩擦力.A、B和滑轮视为质点,不计滑轮质量和滑轮处摩擦,弹簧一直在弹性限度内,g取10m/s2.