题目内容
5. 如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,当人以速度v从平台的边缘处向右匀速前进了位移s,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h,则( )
如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,当人以速度v从平台的边缘处向右匀速前进了位移s,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h,则( )| A. | 在该过程中,物块的运动可能是匀速的 | |
| B. | 在该过程中,人对物块做的功为$\frac{m{v}^{2}{s}^{2}}{2({h}^{2}+{s}^{2})}$ | |
| C. | 在该过程中,人对物块做的功为$\frac{1}{2}$mv2 | |
| D. | 人前进s时,物块的运动速率为$\frac{vh}{\sqrt{{h}^{2}+{s}^{2}}}$ |
分析 对人运动的速度进行分解,分解为沿绳子方向和垂直于绳子方向,在沿绳子方向上的分速度等于物块的速度,根据动能定理求出人对滑块所做的功.
解答 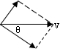 解:A、将人的速度分解为沿绳子方向和垂直于绳子方向,在沿绳子方向上的分速度等于物块的速度,如图,物块的速度等于vcosθ,v不变,θ在变化,所以物块的速度在变化.故A错误.
解:A、将人的速度分解为沿绳子方向和垂直于绳子方向,在沿绳子方向上的分速度等于物块的速度,如图,物块的速度等于vcosθ,v不变,θ在变化,所以物块的速度在变化.故A错误.
B、当人从平台的边缘处向右匀速前进了s,此时物块的速度大小为:
v′=vcosθ=v$\frac{s}{\sqrt{{h}^{2}+{s}^{2}}}$,
根据动能定理得:
W=$\frac{1}{2}$mv′2=$\frac{m{v}^{2}{s}^{2}}{2({h}^{2}+{s}^{2})}$.故C、D错误,B正确.
故选:B.
点评 解决本题的关键知道物块的速度等于绳子收缩的速度,等于人运动的沿绳子方向上的分速度,以及能够灵活运用动能定理.

练习册系列答案
相关题目
1. 如图,在一固定圆柱形磁铁的N极附近放置一平面线圈abcd,磁铁轴线与线圈水平中心线xx′轴重合,则下列说法正确的是( )
如图,在一固定圆柱形磁铁的N极附近放置一平面线圈abcd,磁铁轴线与线圈水平中心线xx′轴重合,则下列说法正确的是( )
 如图,在一固定圆柱形磁铁的N极附近放置一平面线圈abcd,磁铁轴线与线圈水平中心线xx′轴重合,则下列说法正确的是( )
如图,在一固定圆柱形磁铁的N极附近放置一平面线圈abcd,磁铁轴线与线圈水平中心线xx′轴重合,则下列说法正确的是( )| A. | 当线圈刚沿xx′轴向右平移时,线圈中有感应电流 | |
| B. | 当线圈刚绕xx′轴转动时(ad向外,bc向里),线圈中有感应电流 | |
| C. | 当线圈刚沿垂直纸面方向向外平移时,线圈中有感应电流 | |
| D. | 当线圈刚绕yy′轴转动时(ab向里,cd向外),线圈中有感应电流 |
18. 如图所示,1,2,3,…,12各相邻质点的距离均为1m,t=0时,质点1开始向上震动,经过0.1s达到最大位移,且震动向右传播到质点3,则下列说法中正确的是( )
如图所示,1,2,3,…,12各相邻质点的距离均为1m,t=0时,质点1开始向上震动,经过0.1s达到最大位移,且震动向右传播到质点3,则下列说法中正确的是( )
 如图所示,1,2,3,…,12各相邻质点的距离均为1m,t=0时,质点1开始向上震动,经过0.1s达到最大位移,且震动向右传播到质点3,则下列说法中正确的是( )
如图所示,1,2,3,…,12各相邻质点的距离均为1m,t=0时,质点1开始向上震动,经过0.1s达到最大位移,且震动向右传播到质点3,则下列说法中正确的是( )| A. | 波的速度是10m/s,周期是0.4s | |
| B. | 波的频率是2.5Hz,波长是4m | |
| C. | 再经过0.2s振动传至质点7,此时质点5达到最大位移 | |
| D. | 振动传到质点12历时0.6s质点8到达平衡位置 |
10. 从同一地点同时开始沿同一方向做直线运动的两个物体A、B的v-t图象如图所示.在0~t0时间内,下列说法中正确的是( )
从同一地点同时开始沿同一方向做直线运动的两个物体A、B的v-t图象如图所示.在0~t0时间内,下列说法中正确的是( )
 从同一地点同时开始沿同一方向做直线运动的两个物体A、B的v-t图象如图所示.在0~t0时间内,下列说法中正确的是( )
从同一地点同时开始沿同一方向做直线运动的两个物体A、B的v-t图象如图所示.在0~t0时间内,下列说法中正确的是( )| A. | A、B两个物体的加速度大小都在不断减小 | |
| B. | A物体的加速度不断减小,B物体的加速度不断增大 | |
| C. | A、B两物体的位移都不断增大 | |
| D. | A、B两个物体的平均速度大小都大于$\frac{{v}_{1}+{v}_{2}}{2}$ |
14.关于磁铁磁性的起源,安培提出了分子电流假说,他是在怎样的情况下提出的( )
| A. | 安培通过精密仪器观察到了分子电流 | |
| B. | 安培根据环形电流的磁场与磁铁相似而提出的 | |
| C. | 安培根据原子结构理论,进行严格推理得出的 | |
| D. | 安培凭空想出来的 |
 如图所示为一组未知方向的匀强电场的电场线,将带电荷量为q=-1.0×10-6C的点电荷由A点移至B点,克服静电力做了2×10-6J的功,已知A、B间的距离为0.2m.
如图所示为一组未知方向的匀强电场的电场线,将带电荷量为q=-1.0×10-6C的点电荷由A点移至B点,克服静电力做了2×10-6J的功,已知A、B间的距离为0.2m.