题目内容
10. 如图所示,带电平行板长为L,两板间距离为d,板间电压为U,t=0时一质量为m,电荷量为e的电子(重力不计)沿两板中线以速度v0垂直电场方向射入电场,结果被正极板俘获.
如图所示,带电平行板长为L,两板间距离为d,板间电压为U,t=0时一质量为m,电荷量为e的电子(重力不计)沿两板中线以速度v0垂直电场方向射入电场,结果被正极板俘获.(1)简要说明电子在运动过程中的能量转化的情况(不需计算);
(2)当电子速度大小为v时,距正极板多远?
分析 (1)电子在运动的过程中只有电场力做功,电子的动能增大;
(2)结合动能定理即可求出电子速度大小为v时距正极板的距离.
解答 解:(1)电子在运动的过程中只有电场力做功,电子的电势能转化电子的动能,电子的动能增大;根据功能关系可知,电子减少的电势能等于增加的动能.
(2)设当电子速度大小为v时,电子距正极板距离为x,则电子运动的距离为△x=0.5d-x,结合动能定理可得,
$qE•△x=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
其中:$E=\frac{U}{d}$
所以:$x=\frac{1}{2}d-\frac{md}{2qU}({v}^{2}-{v}_{0}^{2})$
答:(1)电子在运动过程中的电势能转化为电子的动能;(2)当电子速度大小为v时,距正极板的距离为$\frac{1}{2}d-\frac{md}{2qU}({v}^{2}-{v}_{0}^{2})$.
点评 该题中,电子的极板之间做类平抛运动,在运动的过程中电场力做正功,电子的电势能减少,动能增大,可以直接使用动能定理或功能关系即可正确解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D面时,下列说法正确的是( )
 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D面时,下列说法正确的是( )| A. | 电场力做功之比为2:1 | B. | 它们的动能之比为2:1 | ||
| C. | 它们所用的时间之比为$\frac{\sqrt{2}}{2}$ | D. | 它们运动的时间之比为$\sqrt{2}$:1 |
1. 图中理想变压器的原、副线圈匝数之比为2:1,电阻R1=R2=10Ω,电表A、V均为理想交流电表.若R1两端电压μ1=10$\sqrt{2}$sin100πt(V),则下列说法正确的有( )
图中理想变压器的原、副线圈匝数之比为2:1,电阻R1=R2=10Ω,电表A、V均为理想交流电表.若R1两端电压μ1=10$\sqrt{2}$sin100πt(V),则下列说法正确的有( )
 图中理想变压器的原、副线圈匝数之比为2:1,电阻R1=R2=10Ω,电表A、V均为理想交流电表.若R1两端电压μ1=10$\sqrt{2}$sin100πt(V),则下列说法正确的有( )
图中理想变压器的原、副线圈匝数之比为2:1,电阻R1=R2=10Ω,电表A、V均为理想交流电表.若R1两端电压μ1=10$\sqrt{2}$sin100πt(V),则下列说法正确的有( )| A. | 电流表的示数为0.5 A | B. | 电压表示数为14.14V | ||
| C. | R1消耗的功率为20W | D. | 原线圈输入交流电频率为50Hz |
5. 木块A、B的重力均为40N,它们与水平地面间的动摩擦因数均为0.25,夹在A、B之间的轻弹簧被压缩了△x=2.0cm,弹簧的劲度系数k=400N/m,系统置于水平地面上静止不动,现用F=10N的水平力推木块B,如图所示,力F作用后( )
木块A、B的重力均为40N,它们与水平地面间的动摩擦因数均为0.25,夹在A、B之间的轻弹簧被压缩了△x=2.0cm,弹簧的劲度系数k=400N/m,系统置于水平地面上静止不动,现用F=10N的水平力推木块B,如图所示,力F作用后( )
 木块A、B的重力均为40N,它们与水平地面间的动摩擦因数均为0.25,夹在A、B之间的轻弹簧被压缩了△x=2.0cm,弹簧的劲度系数k=400N/m,系统置于水平地面上静止不动,现用F=10N的水平力推木块B,如图所示,力F作用后( )
木块A、B的重力均为40N,它们与水平地面间的动摩擦因数均为0.25,夹在A、B之间的轻弹簧被压缩了△x=2.0cm,弹簧的劲度系数k=400N/m,系统置于水平地面上静止不动,现用F=10N的水平力推木块B,如图所示,力F作用后( )| A. | 木块A所受静摩擦力大小为8 N | B. | 弹簧的压缩量变为2.5 cm | ||
| C. | 木块B所受静摩擦力为0 | D. | 木块B所受静摩擦力大小为2.0 N |
 如图所示,是利用闪光照相研究平抛运动的示意图.小球A由斜槽滚下,从桌边缘水平抛出,当它恰好离开桌边缘时,小球B也同时下落,闪光频率为10Hz(每秒拍照10次)的闪光器拍摄的照片中B球有四个像1、2、3、4,间距分别为5cm、15cm、25cm.像间距离已在图中标出,单位为cm,如图所示,两球恰在位置4相碰.(取g=10m/s2)
如图所示,是利用闪光照相研究平抛运动的示意图.小球A由斜槽滚下,从桌边缘水平抛出,当它恰好离开桌边缘时,小球B也同时下落,闪光频率为10Hz(每秒拍照10次)的闪光器拍摄的照片中B球有四个像1、2、3、4,间距分别为5cm、15cm、25cm.像间距离已在图中标出,单位为cm,如图所示,两球恰在位置4相碰.(取g=10m/s2) 如图所示,一质点以初速度v0正对着倾角θ=37°,的斜面水平抛出,空气阻力不计,重力加速度为g,sin37°=0.6,cos37°=0.8,要求质点到达斜面过程很位移最小,求质点在空中飞行的时间t.
如图所示,一质点以初速度v0正对着倾角θ=37°,的斜面水平抛出,空气阻力不计,重力加速度为g,sin37°=0.6,cos37°=0.8,要求质点到达斜面过程很位移最小,求质点在空中飞行的时间t.
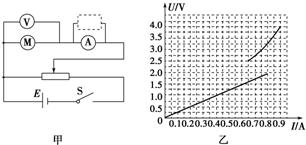 小明、小刚、小敏所在的学习兴趣小组在研究玩具电动机的工作状态时,想描绘出电动机工作时两端电压U和通过电动机线圈的电流I的U-I图线.
小明、小刚、小敏所在的学习兴趣小组在研究玩具电动机的工作状态时,想描绘出电动机工作时两端电压U和通过电动机线圈的电流I的U-I图线.