题目内容
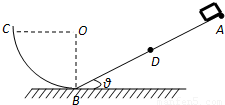
如图所示，倾角θ=30°、长L=2.7m的斜面，底端与一个光滑的1/4圆弧平滑连接，圆弧底端切线水平．一个质量为m=1kg的质点从斜面最高点A沿斜面下滑，经过斜面底端B恰好到达圆弧最高点C，又从圆弧滑回，能上升到斜面上的D点，再由D点由斜面下滑沿圆弧上升，再滑回，这样往复运动，最后停在B点．已知质点与斜面间的动摩擦因数为μ=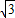
/6，g=10m/s2，假设质点经过斜面与圆弧平滑连接处速率不变．求：（1）质点第1次经过B点时对圆弧轨道的压力；
（2）质点从A到D的过程中质点下降的高度；
（3）质点从开始到第6次经过B点的过程中因与斜面摩擦而产生的热量．
【答案】分析：（1）根据动能定理求出质点第一次到达B点的速度，结合牛顿第二定律和第三定律求出质点对圆弧轨道的压力．
（2）对AB段和BD段分别运用动能定理，求出BD的长度，从而得出质点从A到D的过程中质点下降的高度．
（3）分别对上滑过程和下滑过程运用动能定理，得出上滑的位移与下滑的位移的关系，从而找出规律，得出质点在斜面上运动的路程，通过Q=fs求出产生的热量．
解答：解：（1）设圆弧的半径为R，则质点从C到B过程，由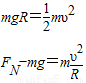
得：FN=3mg=3×1×10N=30N
根据牛顿第三定律，质点第1次经过B点对圆弧轨道的压力为30N．
（2）设质点第一次由B点沿斜面上滑的速度为υ1，B点到D点的距离为L1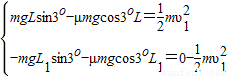
代入数据解得：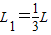
=0.9m
则质点从A点到D点下降的高度h=0.9m
（3）设质点第2次由B点沿斜面上滑的速度为υ2，沿斜面上滑的距离为L2．则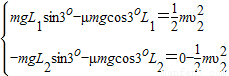
得：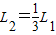
同理可推得：质点第n次由B点沿斜面上滑的距离Ln为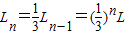
所以质点从开始到第6次经过B点的过程中，在斜面上通过的路程为
S=L+2（L1+L2）=5.1m
Q=μmgcos30°S=12.75J
答：（1）质点第1次经过B点时对圆弧轨道的压力为30N．
（2）质点从A到D的过程中质点下降的高度为0.9m．
（3）质点从开始到第6次经过B点的过程中因与斜面摩擦而产生的热量为12.75J．
点评：本题考查了考查了动能定理和牛顿第二定律，综合性较强，难度中等，关键是理清运动过程，选择合适的过程运用动能定理进行求解．
（2）对AB段和BD段分别运用动能定理，求出BD的长度，从而得出质点从A到D的过程中质点下降的高度．
（3）分别对上滑过程和下滑过程运用动能定理，得出上滑的位移与下滑的位移的关系，从而找出规律，得出质点在斜面上运动的路程，通过Q=fs求出产生的热量．
解答：解：（1）设圆弧的半径为R，则质点从C到B过程，由
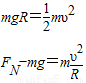
得：FN=3mg=3×1×10N=30N
根据牛顿第三定律，质点第1次经过B点对圆弧轨道的压力为30N．
（2）设质点第一次由B点沿斜面上滑的速度为υ1，B点到D点的距离为L1
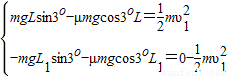
代入数据解得：
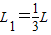=0.9m 则质点从A点到D点下降的高度h=0.9m
（3）设质点第2次由B点沿斜面上滑的速度为υ2，沿斜面上滑的距离为L2．则
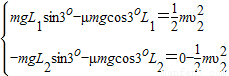
得：
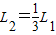
同理可推得：质点第n次由B点沿斜面上滑的距离Ln为
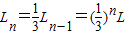
所以质点从开始到第6次经过B点的过程中，在斜面上通过的路程为
S=L+2（L1+L2）=5.1m
Q=μmgcos30°S=12.75J
答：（1）质点第1次经过B点时对圆弧轨道的压力为30N．
（2）质点从A到D的过程中质点下降的高度为0.9m．
（3）质点从开始到第6次经过B点的过程中因与斜面摩擦而产生的热量为12.75J．
点评：本题考查了考查了动能定理和牛顿第二定律，综合性较强，难度中等，关键是理清运动过程，选择合适的过程运用动能定理进行求解．
练习册系列答案
相关题目
如图所示，倾角为37°斜面上方有一小球以一定的速度水平抛出，在空中飞行2s后恰好垂直撞在斜面上，sin37°=0.6，cos37°=0.8，g=10m/s2．求：
如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6m/s的速度运动，运动方向如图所示．一个质量为2kg的物体（物体可以视为质点），从h=3.2m高处由静止沿斜面下滑，物体经过A点时，不管是从斜面到传送带还是从传送带到斜面，都不计其动能损失．物体与传送带间的动摩擦因数为0.5，物体向左最多能滑到传送带左右两端AB的中点处，重力加速度g=10m/s2，求：
（2007?徐州一模）如图所示，倾角θ=37゜的传送带AB长L=20m，以v=5m/s速度沿顺时针方向匀速转动．质量M=lkg的木块由AB的中点c从静止开始下滑，0.5s后被一颗质量 m=20g的子弹以速度v0=500m/s沿传送带向上正对射入，子弹穿出时的速度u=200m/s．以后每隔1.5s就有一颗质量和速度相同的子弹射人木块．设子弹射穿木块的时间极短，且每次射人时木块对子弹的阻力相同．已知木块与传送带间的动摩擦因数μ=0.25，sin37゜=0.60，cos37゜=O．80，g取lOm/s2．求：
（2006?松江区二模）如图所示，倾角θ=30°、宽度L=1m的足够长为U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中，磁场方向垂直导轨平面斜向上．现用一平行导轨的牵引力F，牵引一根质量m=0.2kg、电阻R=1Ω、垂直导轨的金属棒ab，由静止沿导轨向上移动（ab棒始终与导轨接触良好且垂直，不计导轨电阻及一切摩擦）．问：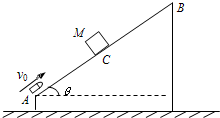
如图所示，倾角θ=37°的固定斜面AB长L=18.4m，质量为M=1kg的木块由斜面中点C从静止开始下滑，0.5s后被一颗质量为m=20g的子弹以v0=500m/s沿斜面向上的速度正对射入并穿出，穿出速度u=200m/s．以后每隔1.0s就有一颗子弹射入木块，设子弹射穿木块的时间极短，且每次射入木块对子弹的阻力相同．已知木块与斜面间的动摩擦因数μ=0.25，g取10m/s2，sin37°=0.60，cos37°=0.80，求：