题目内容
5.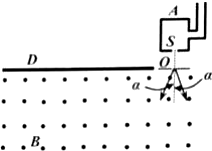 在考古中为了测定古物的年代,可通过测定古物中碳14与碳12的比例,其物理过程可简化为 如图所示,碳14与碳12经电离后的原子核带电量都为q,从容器A下方的小孔S不断飘入电压为U的加 速电场,经过S正下方的小孔O后,沿SO方向垂直 进入磁感应强度为B、方向垂直纸面向外的匀强磁场中,最后打在相机底片D上并被吸收.已知D与O在同一平面内,其中碳12在底片D上的落点到O的距离为x,不考虑粒子重力和粒子在小孔S处的初速度.
在考古中为了测定古物的年代,可通过测定古物中碳14与碳12的比例,其物理过程可简化为 如图所示,碳14与碳12经电离后的原子核带电量都为q,从容器A下方的小孔S不断飘入电压为U的加 速电场,经过S正下方的小孔O后,沿SO方向垂直 进入磁感应强度为B、方向垂直纸面向外的匀强磁场中,最后打在相机底片D上并被吸收.已知D与O在同一平面内,其中碳12在底片D上的落点到O的距离为x,不考虑粒子重力和粒子在小孔S处的初速度. (1)求碳12的比荷
(2)由于粒子间存在相互作用,从O进入磁场的粒子在纸面内将发生不同程度的微小偏转 (粒子进入磁场速度大小的变化可忽略),其方向与竖直方向的最大偏角为α,求碳12在底片D上的落点到O的距离的范围;
(3)实际上,加速电场的电压也会发生微小变化(设电压变化范围为U±△U),从而导致进入磁场的粒子的速度大小也有所不同.现从容器A中飘入碳14与碳12最终均能打在底片D上,若要使这两种粒子的落点区域不重叠,则△U应满足什么条件?(粒子进入磁场时的速 度方向与竖直方向的最大偏角仍为α)
分析 (1)设离子经电场加速度时的速度为v,由动能定理及向心力公式即可求解;
(2)根据半径公式求出粒子在磁场中运动的半径,根据几何关系,确定出粒子在D上的落点与O的距离范围;
(3)根据最大加速电压U+△U,得出落到O点的最大距离,以及根据最小加速电压得出落到O点的最小距离,要使落点区域不重叠,则打中底片时离O点的距离应需满足:碳14的最近距离大于碳12的最远距离,从而求出△U应满足的条件.
解答 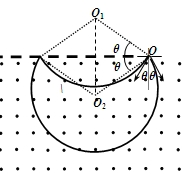 解:(1)加速电场,根据动能定理可得:qU=$\frac{1}{2}m{v}^{2}$①
解:(1)加速电场,根据动能定理可得:qU=$\frac{1}{2}m{v}^{2}$①
根据洛伦兹力提供向心力可得:qvB=m$\frac{{v}^{2}}{r}$②
根据几何关系可得:x=2r③
联立①②③式可得:$\frac{q}{m}$=$\frac{8U}{{B}^{2}{x}^{2}}$④
(2)粒子在磁场中圆运动半径r=$\frac{\sqrt{2qmU}}{qB}$=$\frac{x}{2}$
由图象可知:粒子左偏α角(轨迹圆心为O1)或右偏α角(轨迹圆心为O2)
落点到O的距离相等,均为:L=2Rcosθ
故θ=0°时落点到O的距离最大:Lmax=2R=x
故θ=α时落点到O的距离最小:Lmin=2Rcosα=xcosα
所以:xcosα≤L≤x
(3)联立①②可得:r=$\frac{1}{B}$$\sqrt{\frac{2mU}{q}}$
设碳12的质量为m1,碳14的质量为m2,并且:$\frac{{m}_{1}}{{m}_{2}}$=$\frac{12}{14}$=$\frac{6}{7}$,
根据r=$\frac{1}{B}$$\sqrt{\frac{2mU}{q}}$可知:
碳12的运动半径:r1=$\frac{1}{B}$$\sqrt{\frac{2{m}_{1}U}{q}}$
碳12的最大半径:r1max=$\frac{1}{B}$$\sqrt{\frac{2{m}_{1}(U+△U)}{q}}$
同理:
碳14的运动半径:r2=$\frac{1}{B}$$\sqrt{\frac{2{m}_{2}U}{q}}$
碳14的最小半径:r2min=$\frac{1}{B}$$\sqrt{\frac{2{m}_{2}(U-△U)}{q}}$
若要使这两种粒子的落点区域不重叠,打中底片时离O点的距离应需满足:碳14的最近距离大于碳12的最远距离
即:2r1max<2r2mincosα
联立解得:△U<$\frac{{m}_{2}co{s}^{2}α-{m}_{1}}{{m}_{2}co{s}^{2}α+{m}_{1}}•U$=$\frac{7co{s}^{2}α-6}{7co{s}^{2}α+6}•U$
答:(1)碳12的比荷为$\frac{8U}{{B}^{2}{x}^{2}}$;
(2)碳12在底片D上的落点到O的距离的范围为xcosα≤L≤x;
(3)若要使这两种粒子的落点区域不重叠,则△U应满足△U<$\frac{7co{s}^{2}α-6}{7co{s}^{2}α+6}•U$.
点评 本题考查带电粒子在复合场中的运动,加速场运用动能定理,粒子在磁场中做匀速圆周运动,利用洛伦兹力提供向心力结合几何关系,第三问难点在于找出粒子不重叠的条件,即:打中底片时离O点的距离应需满足:碳14的最近距离大于碳12的最远距离.

| A. | 曲线运动一定具有加速度 | |
| B. | 曲线运动一定不是匀变速运动 | |
| C. | 做曲线运动的物体所受合力可以为零 | |
| D. | 做曲线运动的物体所受合力一定变化 |
| A. | 线速度保持不变 | B. | 向心加速度保持不变 | ||
| C. | 角速度保持不变 | D. | 物体所受合外力保持不变 |

| A. | 甲图是著名的泊松亮斑图案,这是光波的衍射现象 | |
| B. | 乙图中的彩虹是不同色光在水滴中折射率不同造成的 | |
| C. | 丙图的照相机镜头上涂有一层增透膜,增透膜利用了光的偏振原理 | |
| D. | 丁图是医学上的内窥镜,其核心部件光导纤维能传输光像信号,是利用光的全反射 |
 如图所示,绝缘轻弹簧的上端固定在天花板上的O点,下端系一质量为m、电荷量为q的带正电小球,小球套在O点正下方的水平光滑的绝缘杆上,整个装置处于电场强度大小为E,方向沿杆向右的匀强电场中.现将小球从A点由静止释放,运动到B点时与其在A点时的弹簧弹力大小相等,OA=$\frac{4}{5}$OB,在小球从A点运动到B点的过程中,下列判断正确的是( )
如图所示,绝缘轻弹簧的上端固定在天花板上的O点,下端系一质量为m、电荷量为q的带正电小球,小球套在O点正下方的水平光滑的绝缘杆上,整个装置处于电场强度大小为E,方向沿杆向右的匀强电场中.现将小球从A点由静止释放,运动到B点时与其在A点时的弹簧弹力大小相等,OA=$\frac{4}{5}$OB,在小球从A点运动到B点的过程中,下列判断正确的是( )| A. | 小球到达B点时的速度为零 | |
| B. | 小球的电势能一直减小 | |
| C. | 小球的加速度大小为$\frac{qE}{m}$的位置有2个 | |
| D. | 弹簧测力计对小球做功的瞬间功率为零的位置有4个 |
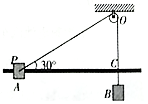 如图,水平光滑长杆上套有质量为m的小物块A,细线一端连接A,另一端跨过转轴为O的轻质小滑轮悬挂质量同为m的小物块B,滑轮到杆的距离为h.将A沿杆拉到P点,使PO与水平方向的夹角为30°,释放A,A、B同时由静止开始运动,则( )
如图,水平光滑长杆上套有质量为m的小物块A,细线一端连接A,另一端跨过转轴为O的轻质小滑轮悬挂质量同为m的小物块B,滑轮到杆的距离为h.将A沿杆拉到P点,使PO与水平方向的夹角为30°,释放A,A、B同时由静止开始运动,则( )| A. | B从释放到第一次达到最低点的过程中,A的动能不断增大 | |
| B. | A由P第一次到达O点正下方的过程中,B的机械能先增大后减小 | |
| C. | 当PO与水平方向的夹角为45°时,A、B速度大小关系是vA=$\frac{\sqrt{2}}{2}$vB | |
| D. | A运动过程中的最大速度为$\sqrt{2gh}$ |
 通电圆环的电流方向如图所示,P点位于垂直圆环且通过圆心的水平直线上,则电流I在P点产生的磁场方向( )
通电圆环的电流方向如图所示,P点位于垂直圆环且通过圆心的水平直线上,则电流I在P点产生的磁场方向( )| A. | 向右 | B. | 向左 | C. | 向上 | D. | 向下 |
