题目内容
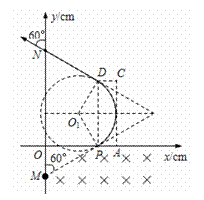
如图所示，第四象限内有互相正交的匀强电场E与匀强磁场B1，E的大小为0.5×103V/m，B1大小为0.5T；第一象限的某个矩形区域内，有方向垂直纸面向里的匀强磁场B2，磁场的下边界与x轴重合．一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动，经P点即进入处于第一象限内的磁场B2区域．一段时间后，小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为(0，-10)，N点的坐标为(0，30)，不计粒子重力，g取10m/s2。
（1）请分析判断匀强电场E的方向（要求在图中画出）并求出微粒的运动速度v；
（2）匀强磁场B2的大小为多大？
（3）B2磁场区域的最小面积为多少？
（1）由于重力忽略不计，微粒在第四象限内仅受电场力和洛仑兹力，且微粒做直线运动，速度的变化会引起洛仑兹力的变化，所以微粒必做匀速直线运动．这样，电场力和洛仑兹力大小相等，方向相反，电场E的方向与微粒运动的方向垂直，即与y轴负方向成60°角斜向下．(在图上表示出也可以得分) （2分）
由力的平衡有：Eq=B1qv （2分）
v=
=
m/s=1.0×103m/s （1分）
（2）画出微粒的运动轨迹如图．
由几何关系可知粒子在第一象限内做圆周运动的半径为 R=
m （2分）
微粒做圆周运动的向心力由洛伦兹力提供，即 
（1分）
解之得 
（1分）
（3）由图可知，磁场B2的最小区域应该分布在图示的矩形PACD内．由几何关系易得PD=2Rsin60°=0.2m （1分）
PA=R（1-cos60°）=
m （1分）
所以，所求磁场的最小面积为 S=
×
=
×=
m2 （1分）
出彩同步大试卷系列答案
（2012?湖南模拟）如图所示，第四象限内有互相正交的电场强度为E的匀强电场与磁感应强度为B1=0.25T的匀强磁场，第一象限的某个矩形区域内，有方向垂直纸面向里、磁感应强度为B：的匀强磁场，磁场的下边界与x轴重合．质量为m=
（2010?南平模拟）（强化班学生做）如图所示，第四象限内有互相正交的匀强电场E与匀强磁场B1，E的大小为0.5×103V/m，B1大小为0.5T．第一象限的某个矩形区域内，有方向垂直纸面向里的匀强磁场B2，磁场的下边界与x轴重合．一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动，经P点即进入处于第一象限内的磁场B2区域．一段时间后，微粒经过y轴上的N点并与y轴正方向成60°角的方向飞出．M点的坐标为（0，-10），N点的坐标为（0，30），不计微粒的重力，g取10m/s2．求：
如图所示，第四象限内有互相正交的匀强电场E与匀强磁场B1，E的大小为0.5×103V/m，B1大小为0.5T；第一象限的某个区域内，有方向垂直纸面向里的匀强磁场B2，磁场B2的下边界与x轴重合．大量的质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒，以某一速度v沿与y轴正方向60°角，从y轴OM间进入B1场，一段时间后，所有的微粒都通过第一象限中的某一点．已知微粒在B1场中沿直线运动，M点的坐标为（0，-10）．不计粒子重力，g取10m/s2．
