题目内容
14. 水平转盘上的A、B、C三个物块如图放置在一条直线上,A、O、B、C在一条直线上,A、B间用一轻质细线相连(开始细线刚好伸直),三个物块与转盘间的动摩擦因数均为μ,质量均为m,到转盘中心O的距离分别为3r、r、2r,现让转盘缓慢加速转动,重力加速度为g,最大静摩擦力等于滑动摩擦力,则( )
水平转盘上的A、B、C三个物块如图放置在一条直线上,A、O、B、C在一条直线上,A、B间用一轻质细线相连(开始细线刚好伸直),三个物块与转盘间的动摩擦因数均为μ,质量均为m,到转盘中心O的距离分别为3r、r、2r,现让转盘缓慢加速转动,重力加速度为g,最大静摩擦力等于滑动摩擦力,则( )| A. | 当物块C相对转盘刚要滑动时,细线张力大小为0.5μmg | |
| B. | 物块C相对转盘刚要滑功时,物块B所受摩擦力大小为μmg | |
| C. | 当细线内刚出现张力时,物块C所受摩擦大小为μmg | |
| D. | 当细线内刚出现张力时,A、B、C所受摩擦力大小为3:1:2 |
分析 当C刚要滑动时,根据牛顿第二定律求出C刚要发生滑动时的临界角速度,再隔离对A、B分析,根据牛顿第二定律求出细线的张力,以及B所受的摩擦力.
当细线刚出现张力时,隔离对A分析,根据牛顿第二定律求出临界的角速度,从而根据牛顿第二定律求出B、C的摩擦力,得出摩擦力大小之比.
解答 解:A、当物块C相对转盘刚要滑动时有:$μmg=m•2r{{ω}_{1}}^{2}$,解得${ω}_{1}=\sqrt{\frac{μg}{2r}}$,对A,根据牛顿第二定律得,$μmg+T=m•3r{{ω}_{1}}^{2}$,解得T=$\frac{1}{2}μmg$,故A正确.
B、物块C刚要滑动时,对B有:$T-{f}_{B}=mr{{ω}_{1}}^{2}$,解得fB=0,故B错误.
C、当细线刚出现张力时,对A,根据牛顿第二定律得,$μmg=m•3r{{ω}_{2}}^{2}$,解得ω2=$\sqrt{\frac{μg}{3r}}$,对C,${f}_{C}=m•2r{{ω}_{2}}^{2}$=$\frac{2}{3}μmg$,故C错误.
D、当细线出现张力时,fA=μmg,${f}_{B}=mr{{ω}_{2}}^{2}=\frac{1}{3}μmg$,${f}_{C}=\frac{2}{3}μmg$,则A、B、C所受的摩擦力大小之比为3:1:2,故D正确.
故选:AD.
点评 解决本题的关键知道物块做圆周运动向心力的来源,抓住临界状态,结合牛顿第二定律进行求解,难度中等.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
4.下列说法正确的是( )
| A. | 只要光足够强,就可以发生光电效应 | |
| B. | 对于同一种金属来说,其极限频率恒定,与入射光的频率及光的强度均无关 | |
| C. | 原子核衰变时,质量数和电荷数都守恒 | |
| D. | 核裂变又叫热核反应 | |
| E. | 每个核子只跟邻近的核子发生核力作用 |
5. 如图所示,斜面倾角为θ的斜面体R静止放在水平地面上,滑块A放在斜面体B上,现用一沿斜面向上的F拉滑块A,在力F的作用下,A、B一起向左沿着水平方向匀速运动,则下列说法正确的是( )
如图所示,斜面倾角为θ的斜面体R静止放在水平地面上,滑块A放在斜面体B上,现用一沿斜面向上的F拉滑块A,在力F的作用下,A、B一起向左沿着水平方向匀速运动,则下列说法正确的是( )
 如图所示,斜面倾角为θ的斜面体R静止放在水平地面上,滑块A放在斜面体B上,现用一沿斜面向上的F拉滑块A,在力F的作用下,A、B一起向左沿着水平方向匀速运动,则下列说法正确的是( )
如图所示,斜面倾角为θ的斜面体R静止放在水平地面上,滑块A放在斜面体B上,现用一沿斜面向上的F拉滑块A,在力F的作用下,A、B一起向左沿着水平方向匀速运动,则下列说法正确的是( )| A. | B对A的摩擦力方向沿着斜面向下 | B. | A和B之间的摩擦力一定不为零 | ||
| C. | 地面对B的摩擦力大小为Fcosθ | D. | 地面对B没有摩擦力的作用 |
6. 在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁的地域风情和人文特色.如图所示,在竖直放置的穹形光滑支架上,一根不可伸长的轻绳(长度足够长)通过轻质光滑滑轮悬挂一重物G.现将轻绳的一端固定于支架上的A点,另一端从C点,沿支架缓慢地向B点靠近,则绳中张力大小变化的情况是( )
在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁的地域风情和人文特色.如图所示,在竖直放置的穹形光滑支架上,一根不可伸长的轻绳(长度足够长)通过轻质光滑滑轮悬挂一重物G.现将轻绳的一端固定于支架上的A点,另一端从C点,沿支架缓慢地向B点靠近,则绳中张力大小变化的情况是( )
 在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁的地域风情和人文特色.如图所示,在竖直放置的穹形光滑支架上,一根不可伸长的轻绳(长度足够长)通过轻质光滑滑轮悬挂一重物G.现将轻绳的一端固定于支架上的A点,另一端从C点,沿支架缓慢地向B点靠近,则绳中张力大小变化的情况是( )
在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁的地域风情和人文特色.如图所示,在竖直放置的穹形光滑支架上,一根不可伸长的轻绳(长度足够长)通过轻质光滑滑轮悬挂一重物G.现将轻绳的一端固定于支架上的A点,另一端从C点,沿支架缓慢地向B点靠近,则绳中张力大小变化的情况是( )| A. | 先变小后变大 | B. | 先不变后变小 | C. | 先不变后变大 | D. | 先变大后变小 |
4.下列说法正确的是( )
| A. | 因为液体表面层分子分布比内部稀疏,因此液体表面有收缩趋势 | |
| B. | 当分子力表现为引力时,分子势能随分子间距离的减小而增大 | |
| C. | 第二类永动机不可能制成,因为它违背能量守恒定律 | |
| D. | 一定质量的理想气体,当它的压强、体积都增大时,其内能一定增加 | |
| E. | 水的饱和汽压随温度的升高而减小 |





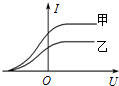 用频率为v但强度不同的甲乙两种光做光电效应实验,发现光电流与电压的关系如图所示,由图可知,甲(选填甲或乙)光的强度大.已知普朗克常量为h,被照射金属的逸出功为W0,则光电子的最大初动能为hγ-W0.
用频率为v但强度不同的甲乙两种光做光电效应实验,发现光电流与电压的关系如图所示,由图可知,甲(选填甲或乙)光的强度大.已知普朗克常量为h,被照射金属的逸出功为W0,则光电子的最大初动能为hγ-W0.