题目内容
2. 如图所示,一个斜面倾角为37°,从斜面顶端沿水平方向抛出一个小石块,初速度大小为v0,它在空中飞行一段时间后又落回斜面,不计空气阻力,(已知sin37°=0.6,cos37°=0.8)
如图所示,一个斜面倾角为37°,从斜面顶端沿水平方向抛出一个小石块,初速度大小为v0,它在空中飞行一段时间后又落回斜面,不计空气阻力,(已知sin37°=0.6,cos37°=0.8)(1)求它从抛出到落在斜面上的运动过程的位移大小;
(2)求它在空中飞行过程中离斜面的最远距离.
分析 (1)根据竖直位移和水平位移的关系,结合运动学公式求出小石块在空中飞行的时间,结合初速度和时间求出位移.
(2)当小石块的速度方向与斜面平行时,小石块到斜面的距离最大,由此即可求出.
解答 解:(1)设运动的时间为t,根据tan37°=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$得小石块在空中飞行的时间为:
t=$\frac{2{v}_{0}tan37°}{g}=\frac{3{v}_{0}}{2g}$.
小石块的水平位移为:
x=v0t=$\frac{3{v}_{0}^{2}}{2g}$
小石块的位移为:
r=$\frac{x}{cos37°}=\frac{15{v}_{0}^{2}}{8g}$
(2)根据平抛运动的特点可知,当小石块的速度方向与斜面平行时,小石块到斜面的距离最大,由运动的对称性可知,到达该点的时间:
$t′=\frac{1}{2}t$
在小石块距离斜面最远点,垂直于斜面方向的速度等于0,所以在垂直于斜面方向的位移:
L=$\frac{{v}_{⊥}}{2}•t′$=$\frac{{v}_{0}sin37°}{2}•t′$=$\frac{9{v}_{0}^{2}}{40g}$
答:(1)它从抛出到落在斜面上的运动过程的位移大小是$\frac{15{v}_{0}^{2}}{8g}$;
(2)它在空中飞行过程中离斜面的最远距离是$\frac{9{v}_{0}^{2}}{40g}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
相关题目
6. 质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )
质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )
 质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )
质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )| A. | 此时物体的速度大小为vsinθ | |
| B. | 此时物体的速度大小为v•cosθ | |
| C. | 汽车对物体做的功为mgh | |
| D. | 汽车对物体做的功为mgh+$\frac{{m(vsinθ)}^{2}}{2}$ |
3.人造地球卫星内有一个质量是1kg的物体,挂在一个弹簧秤上,这时弹簧秤的读数是( )
| A. | 略小于9.8N | B. | 等于9.8N | C. | 略大于9.8N | D. | 0 |
10. 如图所示,两部拖拉机拉着一根原木做匀速直线运动,如果两部拖拉机的拉力之间的夹角始终保持为θ,某段时间内每部拖拉机的拉力对原木所做的功均为W.则在这段时间内,两部拖拉机所做的总功为( )
如图所示,两部拖拉机拉着一根原木做匀速直线运动,如果两部拖拉机的拉力之间的夹角始终保持为θ,某段时间内每部拖拉机的拉力对原木所做的功均为W.则在这段时间内,两部拖拉机所做的总功为( )
 如图所示,两部拖拉机拉着一根原木做匀速直线运动,如果两部拖拉机的拉力之间的夹角始终保持为θ,某段时间内每部拖拉机的拉力对原木所做的功均为W.则在这段时间内,两部拖拉机所做的总功为( )
如图所示,两部拖拉机拉着一根原木做匀速直线运动,如果两部拖拉机的拉力之间的夹角始终保持为θ,某段时间内每部拖拉机的拉力对原木所做的功均为W.则在这段时间内,两部拖拉机所做的总功为( )| A. | 0 | B. | 2W | C. | 2Wcosθ | D. | 2Wsinθ |
11. 甲、乙两种金属发生光电效应时,光电子的最大初动能与入射光频率间的函数关系分别如图中的Ⅰ、Ⅱ所示.下列判断错误的是( )
甲、乙两种金属发生光电效应时,光电子的最大初动能与入射光频率间的函数关系分别如图中的Ⅰ、Ⅱ所示.下列判断错误的是( )
 甲、乙两种金属发生光电效应时,光电子的最大初动能与入射光频率间的函数关系分别如图中的Ⅰ、Ⅱ所示.下列判断错误的是( )
甲、乙两种金属发生光电效应时,光电子的最大初动能与入射光频率间的函数关系分别如图中的Ⅰ、Ⅱ所示.下列判断错误的是( )| A. | 甲金属的逸出功等于Ek1 | |
| B. | 乙金属的极限频率大 | |
| C. | 入射光的频率为2v1时,甲金属产生的光电子的最大初动能为2Ek1 | |
| D. | Ⅰ、Ⅱ的斜率是定值,与入射光和金属材料均无关 |
12.物体做匀变速直线运动的vt图象如图所示.下列说法正确的是( )


| A. | 物体的初速度大小为10 m/s | B. | 物体的初速度大小为20 m/s | ||
| C. | 物体的加速度大小为0.5 m/s2 | D. | 物体的加速度大小为1 m/s2 |
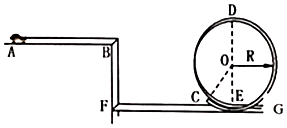 如图所示为一遥控电动赛车(可视为质点)和它运动轨道示意图.假设在某次演示中,赛车从A位置由静止开始运动,经2s后关闭电动机,赛车继续前进至B点后水平飞出,赛车能从C点无碰撞地进入竖直平面内的圆形光滑轨道,D点和E点分别为圆形轨道的最高点和最低点.已知赛车在水平轨道AB段运动时受到的恒定阻力为0.4N,赛车质量
如图所示为一遥控电动赛车(可视为质点)和它运动轨道示意图.假设在某次演示中,赛车从A位置由静止开始运动,经2s后关闭电动机,赛车继续前进至B点后水平飞出,赛车能从C点无碰撞地进入竖直平面内的圆形光滑轨道,D点和E点分别为圆形轨道的最高点和最低点.已知赛车在水平轨道AB段运动时受到的恒定阻力为0.4N,赛车质量 如图所示,在水平恒力F作用下,物体沿光滑曲面从高为h1的A处运动到高为h2的B处,若在A处的速度为vA,B处速度为vB,则AB的水平距离为多大?
如图所示,在水平恒力F作用下,物体沿光滑曲面从高为h1的A处运动到高为h2的B处,若在A处的速度为vA,B处速度为vB,则AB的水平距离为多大? 如图所示,摩托车做特技表演时.以某一速度冲向高台,然后从高台以v0=10m/s的速度水平飞出,人和车的总质量m=200kg,台高h=5m,g取10m/s2.
如图所示,摩托车做特技表演时.以某一速度冲向高台,然后从高台以v0=10m/s的速度水平飞出,人和车的总质量m=200kg,台高h=5m,g取10m/s2.