题目内容
2.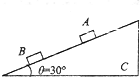 如图所示,斜面C固定在水平地面上,倾角为θ=30°,A、B两物体放在斜面上,距离为d=7.5m,A与C的动摩擦因数为μA=$\frac{1}{2\sqrt{3}}$,B与C的动摩擦因数为μB=$\frac{1}{\sqrt{3}}$,t=0时刻分别给A、B以沿斜面向上的初速度vOA=7.5m/s,vOB=15m/s,取g=10m/s2.求:
如图所示,斜面C固定在水平地面上,倾角为θ=30°,A、B两物体放在斜面上,距离为d=7.5m,A与C的动摩擦因数为μA=$\frac{1}{2\sqrt{3}}$,B与C的动摩擦因数为μB=$\frac{1}{\sqrt{3}}$,t=0时刻分别给A、B以沿斜面向上的初速度vOA=7.5m/s,vOB=15m/s,取g=10m/s2.求:(1)上滑阶段A、B两物体的加速度大小;
(2)从开始到A、B相遇所经历的时间t.
分析 (1)对A、B由于牛顿第二定律求出加速度.
(2)A、B开始都做匀加速直线运动,由于牛顿第二定律求出它们的加速度,然后求出它们减速到零的运动时间,再由于匀变速直线运动的运动规律求出A、B相遇需要的时间.
解答 解:(1)由牛顿第二定律得:
对A:mAgsinθ+μAmAgcosθ=mAaA1,
代入数据解得:aA1=7.5m/s2,
对B:mBgsinθ+μBmBgcosθ=mBaB1,
代入数据解得:aB1=10m/s2;
(2)A、B向上做匀减速直线运动,做减速运动的时间为:
tA=$\frac{{v}_{0A}}{{a}_{A}}$=$\frac{7.5}{7.5}$=1s,
tB=$\frac{{v}_{B}}{{a}_{B}}$=$\frac{15}{10}$=1.5s,
tB>tA,物体A先减速为零,物体A减速为零的过程中:
sA1=$\frac{{v}_{0A}^{2}}{2{a}_{A1}^{\;}}$=$\frac{7.{5}^{2}}{2×7.5}$=3.75m,sB1=v0BtA-$\frac{1}{2}$aB1tA2=15×1-$\frac{1}{2}$×10×12=10m,
d+sA1>sB1,在此过程中A、B没有相遇;
此时A、B间的距离为:s=d+sA1-sB1=7.5+3.75-10=1.25m,
此时B的速度为:vB=v0B-aBtA=15-10×1=5m/s,
由于μA<tanθ,则mAgsinθ>μAmAgcosθ,A速度变为零后将向下做加速运动,
对A,由牛顿第二定律得:mAgsinθ-μAmAgcosθ=mAaA2,
代入数据解得:aA2=2.5m/s2,
当A、B相遇时:s=$\frac{1}{2}$aA2t′2+vBt′-$\frac{1}{2}$aBt′2,
代入数据解得:t′=$\frac{1}{3}$s,
A、B相遇需要的时间为:t=tA+t′=1+$\frac{1}{3}$=$\frac{4}{3}$s;
答:(1)上滑阶段A、B两物体的加速度大小分别为7.5m/s2、10m/s2;
(2)从开始到A、B相遇所经历的时间t为$\frac{4}{3}$s.
点评 本题考查了求加速度、相遇时间问题,由于两物体的运动过程复杂,本题难度较大,分析清楚物体的运动过程是解题的关键,由于牛顿第二定律与运动学公式可以解题.


| A. | 质点在0~6s内位移大小为8m,路程也为8m | |
| B. | 质点在0~8s内位移为-8m,此段时间路程为24m | |
| C. | 0~4s质点的速度为2m/s,4~8s内质点的速度为-4m/s | |
| D. | 质点0~4s向东匀速运动,4~6s向西匀速运动,6~8s向东匀速运动 |

| A. | 图乙是该列波中质点F的振动图线 | |
| B. | 质点G沿x轴正方向移动 | |
| C. | 要使该波能够发生明显的衍射,障碍物的尺寸应小于100cm | |
| D. | 该波与另一列波发生稳定的干涉,则另一列波的频率为2Hz |
 如图甲所示,物体原来静止在水平面上,现用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后做变加速运动,其加速度a随外力F变化的图象如图乙所示,最大静摩擦力略大于滑动摩擦力.根据图乙中的数据可计算出(g=10m/s2)( )
如图甲所示,物体原来静止在水平面上,现用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后做变加速运动,其加速度a随外力F变化的图象如图乙所示,最大静摩擦力略大于滑动摩擦力.根据图乙中的数据可计算出(g=10m/s2)( )| A. | 物体的质量为2 kg | |
| B. | 物体的质量为0.5 kg | |
| C. | 物体与水平面间的动摩擦因数为0.3 | |
| D. | 物体与水平面间的动摩擦因数为0.35 |
 如图所示,物块a、b和c的质量之比为1:2:3,a和b、b和c之间用完全相同的轻弹簧S1和S2相连,通过系在a上的细线悬挂于固定点O,整个系统处于静止状态.现将细线剪断,将物块a、b和c的加速度记为a1、a2和a3,S1和S2相对于原长的伸长量分别记为△l1和△l2,重力加速度大小为g,在剪断的瞬间,下列说法正确的是( )
如图所示,物块a、b和c的质量之比为1:2:3,a和b、b和c之间用完全相同的轻弹簧S1和S2相连,通过系在a上的细线悬挂于固定点O,整个系统处于静止状态.现将细线剪断,将物块a、b和c的加速度记为a1、a2和a3,S1和S2相对于原长的伸长量分别记为△l1和△l2,重力加速度大小为g,在剪断的瞬间,下列说法正确的是( )| A. | a1=6g | B. | a2=2.5g | C. | △l1:△l2=5:3 | D. | △l1:△l2=2:3 |
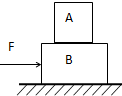 如图所示,木块A质量为1kg,木块B的质量为2kg,叠放在水平地面上,AB间的最大静摩擦力为1N,B与地面间的动摩擦系数为0.1,今用水平力F作用于B,则保持AB相对静止的条件是F不超过( )
如图所示,木块A质量为1kg,木块B的质量为2kg,叠放在水平地面上,AB间的最大静摩擦力为1N,B与地面间的动摩擦系数为0.1,今用水平力F作用于B,则保持AB相对静止的条件是F不超过( )| A. | 1N | B. | 4N | C. | 6N | D. | 8N |
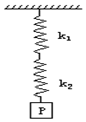 如图所示两个轻质弹簧倔强系数之比为k1:k2=2:1,两弹簧串接后下面悬挂一个重15牛的重物P,平衡后,两弹簧的拉力大小分别为( )
如图所示两个轻质弹簧倔强系数之比为k1:k2=2:1,两弹簧串接后下面悬挂一个重15牛的重物P,平衡后,两弹簧的拉力大小分别为( )| A. | k1和k2的弹力大小均为15牛 | |
| B. | k1和k2的弹力大小均为7.5牛 | |
| C. | k1弹力大小为5牛,k2弹力大小为10牛 | |
| D. | k1弹力大小为10牛,k2弹力大小为5牛 |
| A. | 质量和体积都很大的物体有时也能看成质点 | |
| B. | 体积很小的物体都可以看成质点. | |
| C. | 只有质量和体积都很小的物体才能看成质点 | |
| D. | 质量很小的物体都可以看成质点 |
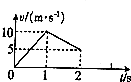 水平地面上质量m=1kg的物体在水平拉力F的作用下运动,t=1s时撤去拉力,
水平地面上质量m=1kg的物体在水平拉力F的作用下运动,t=1s时撤去拉力,