题目内容
13.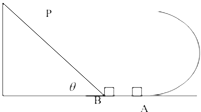 如图所示,在光滑水平地面上有一竖直固定的半径为R的光滑半圆弧轨道和一倾角为θ的表面光滑的斜面体,质量均为m的物体A和B分别放在圆弧轨道和斜面体的底端.
如图所示,在光滑水平地面上有一竖直固定的半径为R的光滑半圆弧轨道和一倾角为θ的表面光滑的斜面体,质量均为m的物体A和B分别放在圆弧轨道和斜面体的底端.(1)要使物体A能够从圆弧的最高点飞出,则A物体的初速度vA至少为多大?
(2)在A物体恰好通过最高点的同时,物体B以vB的初速度沿斜面上滑,当B上滑到最高P点时恰好被A物体击中,则P点到圆弧最高点的水平距离S是多少?(A、B均可看作质点)
分析 (1)物体A恰好能够从圆弧的最高点飞出时,由重力提供向心力,根据牛顿第二定律求出A通过最高点的最小速度,再由机械能守恒定律求出A物体最小的初速度vA.
(2)物体A离开圆弧最高点后做平抛运动,B沿斜面向上做匀减速运动,根据牛顿第二定律求出B的加速度,再由速度时间公式求出B运动的时间,抓住同时性得到A平抛运动的时间,即可结合平抛运动的规律求P点到圆弧最高点的水平距离S.
解答 解:(1)物体A恰好能够从圆弧的最高点飞出时,由重力提供向心力,根据牛顿第二定律得:
mg=m$\frac{{v}_{0}^{2}}{R}$
可得:v0=$\sqrt{gR}$
A从圆弧最低点运动到最高点的过程,由机械能守恒定律得:
mg•2R=$\frac{1}{2}m{v}_{A}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
可得:vA=$\sqrt{5gR}$
即A物体的初速度vA至少为$\sqrt{5gR}$.
(2)物体B沿斜面上滑的加速度大小为:a=$\frac{{m}_{B}gsinθ}{{m}_{B}}$=gsinθ
上滑的时间为:t=$\frac{{v}_{B}}{a}$=$\frac{{v}_{B}}{gsinθ}$
物体A离开圆弧最高点后做平抛运动,则P点到圆弧最高点的水平距离为:S=v0t=$\frac{{v}_{B}\sqrt{gR}}{gsinθ}$
答:(1)A物体的初速度vA至少为$\sqrt{5gR}$.
(2)P点到圆弧最高点的水平距离S为$\frac{{v}_{B}\sqrt{gR}}{gsinθ}$.
点评 解决本题的关键要掌握物体A到达圆弧最高点的临界条件:重力充当向心力,分析时要抓住两个物体运动的同时性.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
1.控制变量法是物理学中研究问题中经常采用的一种研究方法,下列研究问题中属于控制变量法方法的是( )
| A. | 研究电流与电压、电阻的关系 | |
| B. | 在研究磁场时,引入磁感线对磁场进行描述 | |
| C. | 探索磁场对电流的作用规律 | |
| D. | 在研究焦耳定律中电流通过导体产生的热量与通过导体的电流、电阻、时间的关系 |
18.下列有关原子结构和原子核的说法中正确的是( )
| A. | 玻尔理论能很好地解释氢原子光谱 | |
| B. | 某元素的原子核半衰期为4天,则100个该元素的原子核8天后还剩25个 | |
| C. | β射线是高速电子流,证明该射线来自于核外 | |
| D. | 铀核发生裂变后,生成的新核的比结合能比铀核小 |
3.关于光的波粒二象性,下列说法正确的是( )
| A. | 有的光是粒子,有的光是波 | |
| B. | 大量光子的行为表现为粒子性 | |
| C. | 光电效应揭示了光具有粒子性,康普顿效应揭示了光具有波动性 | |
| D. | 光的波长越长,其波动性越明显;波长越短,其粒子性越显著 |
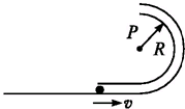 如图所示,半径为R,内径很小的光滑半圆管道竖直放置,质量为m的小球以某一速度进入管内,小球通过最高点P时,对管壁的压力为0,已知重力加速度为g.求:
如图所示,半径为R,内径很小的光滑半圆管道竖直放置,质量为m的小球以某一速度进入管内,小球通过最高点P时,对管壁的压力为0,已知重力加速度为g.求:
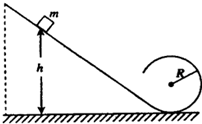 如图所示,位于竖直平面内的光滑轨道,由一段斜的直轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R,一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆轨道运动,要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过7mg(g为重力加速度),求物块初始位置相对于圆形轨道底部的高度h的取值范围.
如图所示,位于竖直平面内的光滑轨道,由一段斜的直轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R,一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆轨道运动,要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过7mg(g为重力加速度),求物块初始位置相对于圆形轨道底部的高度h的取值范围.