题目内容
质量为m、带+q电量的小球以水平初速度v进入竖直向上的匀强电场中，如图甲所示．今测得小球进入电场后在竖直方向上上升的高度y与水平方向的位移x之间的关系如图乙所示．根据图乙给出的信息，求：（1）匀强电场的场强大小；
（2）小球从进入匀强电场到上升到h高度的过程中，电场力所做的功；
（3）小球在h高度处的动能．
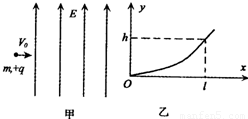
【答案】分析：（1）小球受重力和电场力，在磁场中做类平抛运动，在垂直于磁场方向上做匀速直线运动，在沿电场方向上做匀加速直线运动，根据水平位移求出运动的时间，根据竖直位移求出加速度，再根据牛顿第二定律求出匀强电场的电场强度．
（2）电场力是恒力，根据W=Fscosθ求出恒力的功．
（3）根据动能定理求出小球在h高度处的动能．
解答：解：（1）竖直方向：qE-mg=ma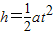
水平方向：l=vt
解得：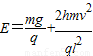
故匀强电场的场强大小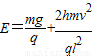
．
（2）W=qEh，代入E得：W=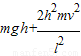
故电场力所做的功为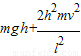
．
（3）由动能定理得：qEh-mgh=Ek-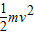
解得：Ek=
+
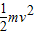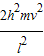
故小球在h高度处的动能为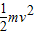
+
．
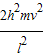点评：解决本题的关键掌握处理类平抛运动的方法，在垂直于磁场方向上做匀速直线运动，在沿电场方向上做匀加速直线运动，且分运动与合运动具有等时性．
（2）电场力是恒力，根据W=Fscosθ求出恒力的功．
（3）根据动能定理求出小球在h高度处的动能．
解答：解：（1）竖直方向：qE-mg=ma
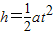
水平方向：l=vt
解得：
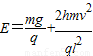
故匀强电场的场强大小
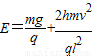．（2）W=qEh，代入E得：W=
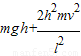
故电场力所做的功为
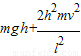．（3）由动能定理得：qEh-mgh=Ek-
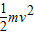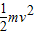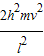
解得：Ek=+故小球在h高度处的动能为
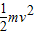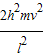+．点评：解决本题的关键掌握处理类平抛运动的方法，在垂直于磁场方向上做匀速直线运动，在沿电场方向上做匀加速直线运动，且分运动与合运动具有等时性．
练习册系列答案
小学期末标准试卷系列答案
相关题目
质量为m、带+q电量的小球以水平初速度v0进入竖直向上的匀强电场中，如图甲所示．今测得小球进入电场后在竖直方向上上升的高度y与水平方向的位移x之间的关系如图乙所示．根据图乙给出的信息，求：
如图所示，一个质量为m，带+q电量的粒子在BC边上的M点以速度v垂直于BC边飞入正三角形ABC．为了使该粒子能在AC边上的N点垂直于AC边飞出该三角形，可在适当的位置加一个垂直于纸面向里、磁感应强度为B的匀强磁场．若此磁场仅分布在一个也是正三角形的区域内，且不计粒子的重力，试求：
一个质量为m，带+q电量的粒子在BC边上的M点以速度v垂直于BC边飞入正三角形ABC．为了使该粒子能在AC边上的N点垂真于AC边飞出该三角形，可在适当的位置加一个垂直于纸面向里，磁感应强度为B的匀强磁场．若此磁场仅分布在一个也是正三角形的区域内，且不计较粒子的重力．试求：
一个质量为m、带+q电量的小球，用长L的绝缘细线悬吊在竖直向下的场强为E的匀强电场中．如果将细线拉至与竖直方向成θ角，然后将小球无初速释放，如图所示．求小球运动到最低点时细线的拉力多大．