题目内容
3. 如图所示,粗细均匀的金属环的电阻为R,可绕轴O转动的金属杆OA的电阻为$\frac{R}{4}$,杆长为l,A端与环相接触,一电阻为$\frac{R}{2}$的定值电阻分别与杆的端点O及环边缘连接.杆OA在垂直于环面向里的、磁感应强度为B的匀强磁场中,以角速度ω顺时针转动.求电路中总电流的变化范围.
如图所示,粗细均匀的金属环的电阻为R,可绕轴O转动的金属杆OA的电阻为$\frac{R}{4}$,杆长为l,A端与环相接触,一电阻为$\frac{R}{2}$的定值电阻分别与杆的端点O及环边缘连接.杆OA在垂直于环面向里的、磁感应强度为B的匀强磁场中,以角速度ω顺时针转动.求电路中总电流的变化范围.
分析 杆OA转动中切割磁感线产生感应电流,同时明确电路结构,根据串并联电路的规律分析电阻的范围,再由闭合电路欧姆定律分析电流的变化范围.
解答  解:设OA杆转至图示位置时,金属环AD间的两部分电阻分别为R1、R2,其等效电路如图所示.
解:设OA杆转至图示位置时,金属环AD间的两部分电阻分别为R1、R2,其等效电路如图所示.
则电路中的总电流为$I=\frac{E}{R_总}=\frac{E}{{\frac{R}{2}+\frac{R}{4}+{R_并}}}=\frac{{\frac{1}{2}Bβω{l^2}}}{{\frac{3}{4}R+{R_并}}}$,式中${R_并}=\frac{{{R_1}{R_2}}}{{{R_1}+{R_2}}}$,因为R1+R2=R为定值,故当R1=R2时,R并有最大值,最大值为$\frac{R}{4}$;
当R1=0或R2=0时,R并有最小值,最小值为0,因此电流的最大值和最小值分别为${I_{min}}=\frac{{\frac{1}{2}Bω{l^2}}}{{\frac{3}{4}R+\frac{1}{4}R}}=\frac{{Bω{l^2}}}{2R}$;
${I_{max}}=\frac{{\frac{1}{2}Bω{l^2}}}{{\frac{3}{4}R+0}}$=$\frac{{2Bω{l^2}}}{3R}$.
所以$\frac{{Bω{l^2}}}{2R}≤I≤\frac{{2Bω{l^2}}}{3R}$.
答:电路中电流的变化范围为$\frac{{Bω{l^2}}}{2R}≤I≤\frac{{2Bω{l^2}}}{3R}$.
点评 本题考查导体切割磁感线与闭合电路欧姆定律的结合应用,要注意本题中明确电路结构是解题的关键,注意圆环两部分相当于并联,总电阻不变,当两边相等时总电阻最大,有一边短路时电阻最小.

 阅读快车系列答案
阅读快车系列答案 有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )
有一体育娱乐比赛项目,其赛道俯视图如图所示,三根长度均为R的拦阻杆的一端固定在水平面上的O点,并能绕O点以角速度ω逆时针匀速转动,拦阻杆间的夹角为120°.AB为拦阻杆转动平面下方的一段水平传送带,传送带以速度v0匀速运动,方向如图所示,拦阻杆能够拦阻传送带的长度为$\sqrt{3}$R.若参赛者从A端踏上传送带,在传送带上不能与拦阻杆相遇,顺利到达B端即为赢得比赛.则参赛者相对传送带的最小运动速度为( )| A. | v=$\frac{3\sqrt{3}Rω+2π{v}_{0}}{2π}$ | B. | v=$\frac{3\sqrt{3}Rω+4π{v}_{0}}{4π}$ | C. | v=$\frac{3\sqrt{3}Rω-4π{v}_{0}}{4π}$ | D. | v=$\frac{3\sqrt{3}Rω}{4π}$ |
| A. | 电源两极间的电压等于电源电动势 | |
| B. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 | |
| C. | 电源电动势的数值等于外电压之和 | |
| D. | 电源电动势与外电路的组成无关 |

| A. | 小物体与甲传送带之间的动摩擦因数比与乙之间的小 | |
| B. | 两传送带对小物体做功相等 | |
| C. | 物体在甲传送带上的重力做功的平均功率比在乙上的大 | |
| D. | 两传送带因与小物体摩擦产生的热量相等 |
| A. | 从外形来判断 | B. | 从各向异性或各向同性来判断 | ||
| C. | 从导电性能来判断 | D. | 从是否具有确定的熔点来判断 |
 质量为的m=1Kg、长度足够长的木板放在光滑的水平面上,右端到竖直档板的距离L=0.08m.现有一质量也为m的滑块以v0=3m/s的水平速度从板的左端滑上木板,滑块与木板间的摩擦系数为μ=0.1,滑块与档板始终未碰撞.木板与档板碰后速度大小不变,方向相反.(碰撞时间极短,忽略不计)则木板碰撞3次后木板与滑块已达到共同速度;木板与档板共碰4次,滑块在木板上发生相对的时间是3s,相对滑动距离是4.5m.
质量为的m=1Kg、长度足够长的木板放在光滑的水平面上,右端到竖直档板的距离L=0.08m.现有一质量也为m的滑块以v0=3m/s的水平速度从板的左端滑上木板,滑块与木板间的摩擦系数为μ=0.1,滑块与档板始终未碰撞.木板与档板碰后速度大小不变,方向相反.(碰撞时间极短,忽略不计)则木板碰撞3次后木板与滑块已达到共同速度;木板与档板共碰4次,滑块在木板上发生相对的时间是3s,相对滑动距离是4.5m.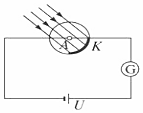 用频率未知的紫外线照射某光电管的阴极时,有光电子飞出.现给你一个电压可调且可指示电压数值的直流电源和一个灵敏度很高的灵敏电流计,试在图的方框中设计一种电路(光电管已画出),要求用该电路测量用所给紫外线照射光电管的阴极时产生的光电子的最大初动能.按照你设计的电路,重要的操作以及需要记录的数据是当加反向电压时,调节滑动触头P,使电流计的示数为零,记录此时电压表的示数U.你所测量的光电子的最大初动能是eU(已知电子电荷量为e).
用频率未知的紫外线照射某光电管的阴极时,有光电子飞出.现给你一个电压可调且可指示电压数值的直流电源和一个灵敏度很高的灵敏电流计,试在图的方框中设计一种电路(光电管已画出),要求用该电路测量用所给紫外线照射光电管的阴极时产生的光电子的最大初动能.按照你设计的电路,重要的操作以及需要记录的数据是当加反向电压时,调节滑动触头P,使电流计的示数为零,记录此时电压表的示数U.你所测量的光电子的最大初动能是eU(已知电子电荷量为e).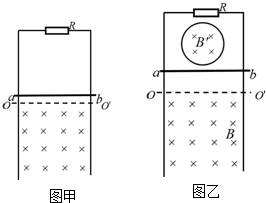
 粗细均匀的两端开口的U形细玻璃管开口向下竖直放置时,在左、右管中各有长度是L的水银柱封闭住总长是8L的气柱A,如图,左、右管之间的距离忽略不计,左、右管长度都是6L,两水银柱的下表面到管口距离相等.大气压保持为p=4ρgL,ρ是水银的密度,g是重力加速度.把一侧的管口封住(不计厚度),再缓慢转动U形管,使其开口向上竖直放置,两侧水银柱的长度不变.
粗细均匀的两端开口的U形细玻璃管开口向下竖直放置时,在左、右管中各有长度是L的水银柱封闭住总长是8L的气柱A,如图,左、右管之间的距离忽略不计,左、右管长度都是6L,两水银柱的下表面到管口距离相等.大气压保持为p=4ρgL,ρ是水银的密度,g是重力加速度.把一侧的管口封住(不计厚度),再缓慢转动U形管,使其开口向上竖直放置,两侧水银柱的长度不变.