题目内容
10.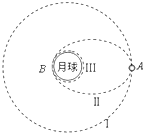 “神州七号”飞船的成功飞行为我国在2010年实现探月计划-“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )
“神州七号”飞船的成功飞行为我国在2010年实现探月计划-“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )| A. | 飞船在轨道Ⅰ上的运行速率v=$\frac{1}{2}$$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在A点处点火时,动能增加 | |
| C. | 飞船在轨道Ⅰ上运行速率大于在轨道Ⅲ上的运行速率 | |
| D. | 飞船在轨道Ⅲ绕月球运行一周所需的时间为T=2π$\sqrt{\frac{R}{{g}_{0}}}$ |
分析 飞船圆周运动的向心力由万有引力提供,掌握飞船通过做近心运动改变轨道高度,根据运动条件判断飞船的运动情况.
解答 解:A、设月球的质量为M,飞船的质量为m,飞船绕月运动速度为v,由万有引力提供向心力:$\frac{GMm}{(4R)^{2}}=m\frac{{v}^{2}}{4R}$,又:GM=g0R2,解得:v=$\frac{1}{2}\sqrt{{g}_{0}R}$,故A正确;
B、由图可知点火后由原来的高轨道Ⅰ进入低轨道Ⅱ,可知卫星要减速,故B错误;
C、根据万有引力提供圆周运动向心力知$G\frac{mM}{{R}^{2}}=m\frac{{v}^{2}}{R}$可得线速度$v=\sqrt{\frac{GM}{R}}$可知轨道半径小的线速度大,故C错误;
D、在近地轨道II上运动时轨道半径为R,此时满足万有引力等于重力并提供飞船运动的向心力有$G\frac{mM}{{R}^{2}}=m{g}_{0}=mR\frac{4{π}^{2}}{{T}^{2}}$,由此可得飞船在轨道III上的周期T=$2π\sqrt{\frac{R}{{g}_{0}}}$,所以D正确.
故选:AD.
点评 主要考查圆周运动中各种向心力公式的变换.注意题设条件的完整性.掌握万有引力提供圆周运动向心力的灵活运用,并了解飞船变轨原理是解决问题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
1. 如图所示,电源电动势E=8V,内电阻为r=0.5Ω,“3V,3W”的灯泡L与电动机M串联接在电源上,灯泡刚好正常发光,电动机刚好正常工作,电动机的线圈电阻R0=1.5Ω.下列说法中正确的是( )
如图所示,电源电动势E=8V,内电阻为r=0.5Ω,“3V,3W”的灯泡L与电动机M串联接在电源上,灯泡刚好正常发光,电动机刚好正常工作,电动机的线圈电阻R0=1.5Ω.下列说法中正确的是( )
 如图所示,电源电动势E=8V,内电阻为r=0.5Ω,“3V,3W”的灯泡L与电动机M串联接在电源上,灯泡刚好正常发光,电动机刚好正常工作,电动机的线圈电阻R0=1.5Ω.下列说法中正确的是( )
如图所示,电源电动势E=8V,内电阻为r=0.5Ω,“3V,3W”的灯泡L与电动机M串联接在电源上,灯泡刚好正常发光,电动机刚好正常工作,电动机的线圈电阻R0=1.5Ω.下列说法中正确的是( )| A. | 通过电动机的电流为1.6 A | B. | 电源的输出功率是8 W | ||
| C. | 电动机消耗的电功率为3 W | D. | 电动机的输出功率为3 W |
5.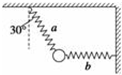 如图所示,两轻质弹簧a、b悬挂一质量为m的小铁球,小铁球处于平衡状态,a弹簧与竖直方向成30°角,b弹簧水平,a、b两弹簧的劲度系数分别为k1、k2,重力加速度为g,则下列说法正确的是( )
如图所示,两轻质弹簧a、b悬挂一质量为m的小铁球,小铁球处于平衡状态,a弹簧与竖直方向成30°角,b弹簧水平,a、b两弹簧的劲度系数分别为k1、k2,重力加速度为g,则下列说法正确的是( )
 如图所示,两轻质弹簧a、b悬挂一质量为m的小铁球,小铁球处于平衡状态,a弹簧与竖直方向成30°角,b弹簧水平,a、b两弹簧的劲度系数分别为k1、k2,重力加速度为g,则下列说法正确的是( )
如图所示,两轻质弹簧a、b悬挂一质量为m的小铁球,小铁球处于平衡状态,a弹簧与竖直方向成30°角,b弹簧水平,a、b两弹簧的劲度系数分别为k1、k2,重力加速度为g,则下列说法正确的是( )| A. | a弹簧的伸长量为$\frac{\sqrt{3}mg}{3{k}_{1}}$ | |
| B. | a、b两弹簧的伸长量的比值为$\frac{2{k}_{2}}{{k}_{1}}$ | |
| C. | 若弹簧b的左端松脱,则松脱瞬间小铁球的加速度为$\frac{g}{2}$ | |
| D. | 若弹簧a的下端松脱,则松脱瞬间小铁球的加速度为$\sqrt{3}$g |
15.关于功、功率和机械能,以下说法中正确的是( )
| A. | 一对相互作用的静摩擦力同时做正功、同时做负功、同时不做功都是可能的 | |
| B. | 物体做曲线运动时,其合力的瞬时功率不可能为零 | |
| C. | 物体受合外力为零时,其动能不变,但机械能可能改变 | |
| D. | 雨滴下落时,所受空气阻力的功率越大,其动能变化就越快 |
2.某物体运动的v-t图象如图所示,则下列说法正确的是( )


| A. | 物体在第1s 末运动方向发生改变 | |
| B. | 物体在第2s内和第3s内的加速度是相同的 | |
| C. | 物体在第6s末返回出发点 | |
| D. | 在t=0~t=6s这段时间内物体的平均速度为0.5m/s |
19. 如图所示,把重为20N的物体放在倾角θ=30°的粗糙斜面上并静止,物体右端与固定在斜面上的轻弹簧相连接(弹簧与斜面平行),若物体与斜面间的最大静摩擦力为12N,则弹簧对物体的弹力不可能的是( )
如图所示,把重为20N的物体放在倾角θ=30°的粗糙斜面上并静止,物体右端与固定在斜面上的轻弹簧相连接(弹簧与斜面平行),若物体与斜面间的最大静摩擦力为12N,则弹簧对物体的弹力不可能的是( )
 如图所示,把重为20N的物体放在倾角θ=30°的粗糙斜面上并静止,物体右端与固定在斜面上的轻弹簧相连接(弹簧与斜面平行),若物体与斜面间的最大静摩擦力为12N,则弹簧对物体的弹力不可能的是( )
如图所示,把重为20N的物体放在倾角θ=30°的粗糙斜面上并静止,物体右端与固定在斜面上的轻弹簧相连接(弹簧与斜面平行),若物体与斜面间的最大静摩擦力为12N,则弹簧对物体的弹力不可能的是( )| A. | 可以为22N,方向沿斜面向上 | B. | 可以为2N,方向沿斜面向上 | ||
| C. | 可以为12N,方向沿斜面向下 | D. | 弹力可能为零 |
 如图所示,物体的质量m=2kg,与水平地面间的动摩擦因数μ=0.3,在倾角为37°、F=10N的推力作用下,由静止开始加速运动,当t=10s时撒去F,(sin37°=0.6 cos37°=0.8)求:
如图所示,物体的质量m=2kg,与水平地面间的动摩擦因数μ=0.3,在倾角为37°、F=10N的推力作用下,由静止开始加速运动,当t=10s时撒去F,(sin37°=0.6 cos37°=0.8)求:
 如图,线圈的面积是0.05m2,共100匝,线圈总电阻为1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度为B=$\frac{1}{π}T$,当线圈以300r/min的转速匀速旋转时,求:
如图,线圈的面积是0.05m2,共100匝,线圈总电阻为1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度为B=$\frac{1}{π}T$,当线圈以300r/min的转速匀速旋转时,求: