题目内容
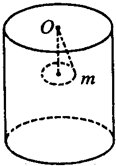 如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为FT=2mg,小球在水平面内做圆周运动,当小球速度慢慢地逐渐增大到绳断裂后,小球恰好以速度v2=
如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为FT=2mg,小球在水平面内做圆周运动,当小球速度慢慢地逐渐增大到绳断裂后,小球恰好以速度v2=| 7gL |
(1)绳断裂瞬间小球的速度v1
(2)绳断裂瞬间小球地面的竖直高度h
(3)圆柱形房屋的半径R.
分析:(1)小球在水平面内做匀速圆周运动时,由重力和绳子拉力的合力提供向心力,根据牛顿第二定律求解速度v1;
(2)、(3)小球在绳子断开后做平抛运动,根据动能定理求得小球下落的高度h,由平抛运动的规律和几何知识求解半径R.
(2)、(3)小球在绳子断开后做平抛运动,根据动能定理求得小球下落的高度h,由平抛运动的规律和几何知识求解半径R.
解答:解:(1)绳断裂瞬间,对小球的受力分析(如下图),根据牛顿第二定 律,有:
律,有:
FTcosθ=mg…①
FTsinθ=m
…②
且 FT=2mg…③
r=Lsinθ…④
联①②③④式,代入数据解得:θ=60°,v1=
…⑤
(2)小球从抛出至落地,由动能定理有:mgh=
m
-
m
…⑥
代入数据,解得:h=
L…⑦
(3)绳断后,小球做平抛运动,且有:
h=
gt2…⑧
x=v1t…⑨
R=
…⑩
解得:R=3L…(11)
答:(1)绳断裂瞬间小球的速度v1是
.
(2)绳断裂瞬间小球地面的竖直高度h是
L.
(3)圆柱形房屋的半径R是3L.
 律,有:
律,有:FTcosθ=mg…①
FTsinθ=m
| ||
| r |
且 FT=2mg…③
r=Lsinθ…④

联①②③④式,代入数据解得:θ=60°,v1=
|
(2)小球从抛出至落地,由动能定理有:mgh=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
代入数据,解得:h=
| 9 |
| 4 |

(3)绳断后,小球做平抛运动,且有:
h=
| 1 |
| 2 |
x=v1t…⑨
R=
| (Lsinθ)2+x2 |
解得:R=3L…(11)
答:(1)绳断裂瞬间小球的速度v1是
|
(2)绳断裂瞬间小球地面的竖直高度h是
| 9 |
| 4 |
(3)圆柱形房屋的半径R是3L.
点评:本题主要考查了平抛运动的基本公式及向心力公式的应用,要求同学们能画出小球运动的轨迹,能结合几何关系解题,难度适中.

练习册系列答案
相关题目
 如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2=
如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2=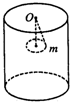 如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2=
如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2= 落到墙脚边.求
落到墙脚边.求
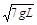 落到墙脚边.求
落到墙脚边.求