题目内容
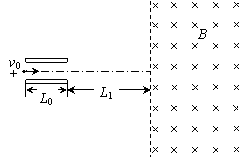
如图,真空中有一个平行板电容器,极板长L0=10cm,间距d=![]() cm,两极板接在电压u=200sin(100πt )V的交流电源上,在平行板电容器右端L1=20cm处有一个范围足够大的匀强磁场,磁场方向垂直纸面向里,磁感应强度为B=
cm,两极板接在电压u=200sin(100πt )V的交流电源上,在平行板电容器右端L1=20cm处有一个范围足够大的匀强磁场,磁场方向垂直纸面向里,磁感应强度为B=![]() ×10-2T.一束带正电的粒子以v0=
×10-2T.一束带正电的粒子以v0= ![]() ×105m/s的速度沿着两极板的中轴线飞入电场,粒子的比荷q/m=1×108C/kg,不计粒子的重力.问:
×105m/s的速度沿着两极板的中轴线飞入电场,粒子的比荷q/m=1×108C/kg,不计粒子的重力.问:
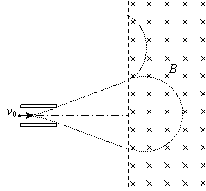
(1)何时飞入的粒子在电场中不发生偏转?这样的粒子进入磁场的深度多大?
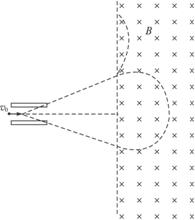
(2)何时飞入的粒子在离开电场时偏转最大?这样的粒子进入磁场的深度多大?
(3)第(2)问中的粒子从飞入电场到离开磁场经过的总时间为多大?
解析:(1)粒子飞越电场的时间t0= L0/ v0 t0=(![]() /3) ×10-6s T=0.02s t0<< T
/3) ×10-6s T=0.02s t0<< T
所以,每个粒子飞越电场的过程中,可以认为此时的电场是恒定的,要在电场中不偏转,条件是u=0 即![]() 100πt=nπ n=0、1、2、3…
100πt=nπ n=0、1、2、3…
所以进入的时刻为:t=n/100s
或 t1=0、10-2 s、2×10-2 s、3×10-2 s、4×10-2s...
在磁场中有B v0q=m v02/R R= m v0/Bq R=0.1m 即深度
(2)粒子飞越电场的最大偏转距离最多为d/2 假设这时的电压为U0
![]() =
=![]() U0 =
U0 =![]() 代入得:U0=100V
代入得:U0=100V
由100=200sin100пt 并考虑到对称性可得:t=![]()
或 t2=![]() ×10-2 s、(1
×10-2 s、(1![]()
![]() )×10-2 s、(2
)×10-2 s、(2![]()
![]() )×10-2 s、(3
)×10-2 s、(3![]()
![]() )×10-2 s、...
)×10-2 s、...
粒子的出射角度tan![]() =
=![]() =
=![]() tan
tan![]() =
=![]()
![]() =300
=300
出射速度v= ![]() R/ =
R/ =![]() R/=
R/=![]() cm
cm
打入深度D= R/(1+sin![]() ) D=10
) D=10![]() cm
cm
考虑到向上偏转的情况,打入深度D’= R’ (1-sin![]() )
)
D’=![]() cm
cm
(3)在电场和磁场之间飞行时间t3=![]() t3=
t3=![]() ×10-6s 在磁场中的飞行时间
×10-6s 在磁场中的飞行时间
 t4=2T/3 T=
t4=2T/3 T=![]() t4=
t4=![]() t总= t0+t3+t4=
t总= t0+t3+t4=![]() (1+
(1+![]() )×10-6s
)×10-6s
考虑到向上偏转的情况,在磁场中的飞行时间t5 =T/3
t’总= t0+t3+t5=![]() (1+
(1+![]() )×10-6s
)×10-6s

 口算能手系列答案
口算能手系列答案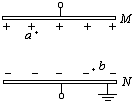 如图所示,在真空中有一平行板电容器,两板间距离为10cm,a点离M板2cm,b点离N板也是2cm,ab两点在平行于极板方向的距离为6cm.当电容器充电后,M板带正电荷,N板带负电荷,现测得一个电荷量为+2×10-8C的点电荷,放在a点时所受的电场力大小为2×10-5N,则:该电容器两板间的电势差大小为
如图所示,在真空中有一平行板电容器,两板间距离为10cm,a点离M板2cm,b点离N板也是2cm,ab两点在平行于极板方向的距离为6cm.当电容器充电后,M板带正电荷,N板带负电荷,现测得一个电荷量为+2×10-8C的点电荷,放在a点时所受的电场力大小为2×10-5N,则:该电容器两板间的电势差大小为