题目内容
13. 一个10kg的猴子爬上根无质绳,绳子跨过无摩擦的树枝连到地面上一个15kg的箱子上(见图).
一个10kg的猴子爬上根无质绳,绳子跨过无摩擦的树枝连到地面上一个15kg的箱子上(见图).(1)为了能提起地面的箱子,猴子向上爬的最小加速度大小是多少?
(2)如果箱子被拉起之后猴子停止爬动而抓着绳,那么猴子加速度的大小是多少?方向如何?,此时绳子中的张力多大?
第(1)问提示:要把地上的箱子提起绳上的张力至少应达多少?
分析 (1)当猴子以最小加速度向上爬行时,箱子对地压力为零,故猴子对细绳的拉力等于箱子的重力,对猴子受力分析,运用牛顿第二定律求解加速度;
(2)如果箱子被拉起之后猴子停止爬动而抓着绳,之后只受重力和绳的拉力影响,猴子和箱子做加速度大小相同方向相反的匀加速运动,比较重力大小确定运动方向,根据牛顿第二定律求出张力.
解答 解:设猴子的质量为m,箱子的质量为M.
(1)猴子以最小加速度向上爬行时,箱子对地压力为零,
故猴子对细绳的拉力等于箱子的重力,即:F=Mg;
猴子对细绳的拉力等于细绳对猴子的拉力:F′=F;
对猴子受力分析,受重力和拉力,根据牛顿第二定律,有
F′-mg=ma
代入数据解得:a=5m/s2
(2)猴子和箱子只受重力和绳的拉力影响,做连体运动,设加速度大小为a,绳的拉力为T,
由于箱子的重力大于猴子的重力,故箱子做竖直向下的匀加速运动,猴子做竖直向上的匀加速运动;
根据牛顿第二定律
对箱子:Mg-T=Ma
对猴子:T=ma
联立以上两式代入数据得:T=60N,a=6m/s2
故猴子加速度的大小为6m/s2,方向为竖直向上,绳子的张力为60N.
答:(1)最小加速度为5m/s2;
(2)猴子加速度的大小是6m/s2,方向为竖直向上,此时绳子中的张力为60N.
点评 本题关键先后对重物和小猴受力分析,然后根据共点力平衡条件和牛顿第二定律列式求解.

练习册系列答案
相关题目
3.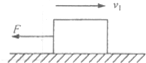 在水平地面上小物块经过如图所示的位置时,速度大小为v1、方向水平向右,若立即对小物块施加水平向左的恒力F,经过一段时间后小物块再次回到图示位置,速度大小为v2、方向水平向左,且v2<v1.已知F=kmg,则小物块与水平地面之间的动摩擦因数为( )
在水平地面上小物块经过如图所示的位置时,速度大小为v1、方向水平向右,若立即对小物块施加水平向左的恒力F,经过一段时间后小物块再次回到图示位置,速度大小为v2、方向水平向左,且v2<v1.已知F=kmg,则小物块与水平地面之间的动摩擦因数为( )
 在水平地面上小物块经过如图所示的位置时,速度大小为v1、方向水平向右,若立即对小物块施加水平向左的恒力F,经过一段时间后小物块再次回到图示位置,速度大小为v2、方向水平向左,且v2<v1.已知F=kmg,则小物块与水平地面之间的动摩擦因数为( )
在水平地面上小物块经过如图所示的位置时,速度大小为v1、方向水平向右,若立即对小物块施加水平向左的恒力F,经过一段时间后小物块再次回到图示位置,速度大小为v2、方向水平向左,且v2<v1.已知F=kmg,则小物块与水平地面之间的动摩擦因数为( )| A. | $\frac{{v}_{1}^{2}+{v}_{2}^{2}}{k({v}_{1}^{2}-{v}_{2}^{2})}$ | B. | $\frac{k({v}_{1}^{2}+{v}_{2}^{2})}{{v}_{1}^{2}-{v}_{2}^{2}}$ | ||
| C. | $\frac{{v}_{1}^{2}-{v}_{2}^{2}}{k({v}_{1}^{2}+{v}_{2}^{2})}$ | D. | $\frac{k({v}_{1}^{2}-{v}_{2}^{2})}{{v}_{1}^{2}+{v}_{2}^{2}}$ |
18.平伸手拿托起物体,由静止开始竖直向上运动,直至将物体抛出.下列说法正确的是( )
| A. | 手托物体向上运动的过程中,物体始终处于超重状态 | |
| B. | 手托物体向上运动的过程中,物体始终处于失重状态 | |
| C. | 在物体离开手的瞬间,物体的加速度大于重力加速度 | |
| D. | 在物体离开手的瞬间,手的加速度大于重力加速度 |
2.关于磁感线的概念和性质,以下说法中正确的是( )
| A. | 磁感线上各点的切线方向就是小磁针静止时北极的指向 | |
| B. | 磁场中任意两条磁感线有可能相交 | |
| C. | 铁屑在磁场中的分部所形成的曲线就是实际存在的磁感线 | |
| D. | 磁感线总是从磁体的N极发出终止于磁体的S极 |
3.物体静止放在水平桌面上,则( )
| A. | 物体对桌面的压力与物体受到的重力是同一个力,性质相同 | |
| B. | 桌面对物体的支持力与物体对桌面的压力是一对作用力与反作用力 | |
| C. | 桌面对物体的支持力与物体受到的重力是一对平衡力 | |
| D. | 物体对桌面的压力是桌面发生形变产生的 |
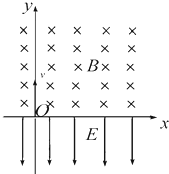 如图所示,在x轴上方有垂直于xy平面向里的匀强磁场,磁感应强度为B;在x轴下方有沿y轴负方向的匀强电场,场强为E.一质量为m,电量为-q的粒子从坐标原点O沿着y轴正方向射出?射出之后,第三次到达x轴时(O点不算第一次),它与点O的距离为L.求:
如图所示,在x轴上方有垂直于xy平面向里的匀强磁场,磁感应强度为B;在x轴下方有沿y轴负方向的匀强电场,场强为E.一质量为m,电量为-q的粒子从坐标原点O沿着y轴正方向射出?射出之后,第三次到达x轴时(O点不算第一次),它与点O的距离为L.求: 如图所示,质量为m的物块A被轻质细绳系住斜吊着放在倾角为30°的静止斜面上,物块A与斜面间的动摩擦因数μ(μ<$\frac{\sqrt{3}}{3}$),细绳绕过定滑轮O,左右两边与竖直方向的夹角α=30°、β=60°,细绳右端固定在天花板上,O′为细绳上一光滑动滑轮,下方悬挂着重物B.整个装置处于静止状态,重力加速度为g,最大静摩擦力近似等于滑动摩擦力,不考虑动滑轮重力,求:
如图所示,质量为m的物块A被轻质细绳系住斜吊着放在倾角为30°的静止斜面上,物块A与斜面间的动摩擦因数μ(μ<$\frac{\sqrt{3}}{3}$),细绳绕过定滑轮O,左右两边与竖直方向的夹角α=30°、β=60°,细绳右端固定在天花板上,O′为细绳上一光滑动滑轮,下方悬挂着重物B.整个装置处于静止状态,重力加速度为g,最大静摩擦力近似等于滑动摩擦力,不考虑动滑轮重力,求: 在地面上有竖直放置的静止物体A和B,A、B之间用不计质量的轻弹簧栓接在一起,弹簧的劲度系数k=100N/m,A、B的质量都为1kg,现用F=20N的竖直向上恒力作用在物体A上,使A竖直上升,重力加速度g=10m/s2,设弹簧始终是在弹性限度内,空气阻力不计.求
在地面上有竖直放置的静止物体A和B,A、B之间用不计质量的轻弹簧栓接在一起,弹簧的劲度系数k=100N/m,A、B的质量都为1kg,现用F=20N的竖直向上恒力作用在物体A上,使A竖直上升,重力加速度g=10m/s2,设弹簧始终是在弹性限度内,空气阻力不计.求 如图所示,正方形匀强磁场的边界长为a,边界由绝缘弹性壁围成,磁场的磁感应强度为B,质量为m、电荷量为q的带正电粒子垂直于磁场方向和边界从边界正中点O处射入磁场,其射入时的速度为$\frac{17Bqa}{8m}$,带电粒子与壁碰撞前后沿壁方向的分速度不变,垂直壁方向的分速度反向、大小不变,且不计摩擦,不计粒子所受重力,碰撞时无电荷量损失,求:
如图所示,正方形匀强磁场的边界长为a,边界由绝缘弹性壁围成,磁场的磁感应强度为B,质量为m、电荷量为q的带正电粒子垂直于磁场方向和边界从边界正中点O处射入磁场,其射入时的速度为$\frac{17Bqa}{8m}$,带电粒子与壁碰撞前后沿壁方向的分速度不变,垂直壁方向的分速度反向、大小不变,且不计摩擦,不计粒子所受重力,碰撞时无电荷量损失,求: