题目内容
如图所示的玻璃砖为半径为R的半圆形玻璃砖上截取的一部分，其折射率为n，一束光线垂直于AB边入射，当人射点P距AB边中点至少为多远时，曲面上将无光线透射？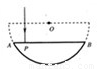
【答案】分析：当射到曲面上的光线发生全反射时将无光线透射．由sinC=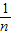
求出临界角C．画出光路图，由几何关系求出人射点P距AB边中点的最小距离．
解答：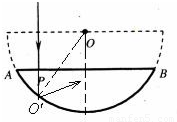
解：当射到曲面上的光线发生全反射时将无光线透射．设玻璃的临界角为C，则sinC=
．
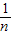图中∠PO′O=C，即sin∠PO′O=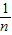
．
设入射点P距AB边中点的距离为L，由几何知识得
sin∠PO′O=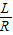
联立解得，L=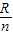
当人射点P距AB边中点至少为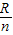
时，曲面上将无光线透射．
答：当人射点P距AB边中点至少为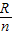
时，曲面上将无光线透射．
点评：本题关键要掌握全反射的条件和临界角的公式，结合几何知识求解．
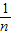求出临界角C．画出光路图，由几何关系求出人射点P距AB边中点的最小距离．解答：
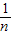解：当射到曲面上的光线发生全反射时将无光线透射．设玻璃的临界角为C，则sinC=．图中∠PO′O=C，即sin∠PO′O=
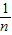．设入射点P距AB边中点的距离为L，由几何知识得
sin∠PO′O=
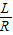
联立解得，L=
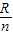
当人射点P距AB边中点至少为
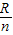时，曲面上将无光线透射．答：当人射点P距AB边中点至少为
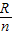时，曲面上将无光线透射．点评：本题关键要掌握全反射的条件和临界角的公式，结合几何知识求解．
练习册系列答案
阅读快车系列答案
相关题目
（2013?罗山县一模）如图所示，AOB为半圆形玻璃砖截面，玻璃的折射率为n=
如图所示，半径为R的半圆柱形玻璃砖，放置在直角坐标系xOy中，圆心与坐标系原点O重合．在第二象限中坐标为（-1.5R，
（1）下列说法中正确的是
用如图所示的装置观察光的反射和折射现象，并测得玻璃的折射率，在光具盘的中央固定一块半圆柱形玻璃砖，使二者的圆心O重合，使激光束从玻璃圆弧面一侧入射，并垂直直径平面通过圆心O沿直线射出玻璃砖，记下入射光束在光具盘上对应位置的刻度，以圆心为轴，入射光束方向不变，逆时针缓慢转动光具盘，同时发现有两束光在光具盘上移动，其中从玻璃弧面射出的光束沿