题目内容
17. 过山翻滚车是一种常见的游乐项目,如图是螺旋形过山翻滚车的轨道,一质量为100kg的小车从高为14m处由静止滑下,当它通过半径为R=4m的竖直平面内圆轨道的最高点A时,对轨道的压力的大小恰等于车重,求小车通过A点时的速度?(g取10m/s2)
过山翻滚车是一种常见的游乐项目,如图是螺旋形过山翻滚车的轨道,一质量为100kg的小车从高为14m处由静止滑下,当它通过半径为R=4m的竖直平面内圆轨道的最高点A时,对轨道的压力的大小恰等于车重,求小车通过A点时的速度?(g取10m/s2)
分析 在圆形轨道最高点A,由重力和轨道的压力的合力提供小球的向心力,由牛顿第二定律求出小球通过最高点时的速度.
解答 解:在圆形轨道最高点,根据牛顿第二定律得:
mg+N=m$\frac{{v}_{A}^{2}}{R}$
据题得:N=mg
联立得:vA=$\sqrt{2gR}$=$\sqrt{2×10×4}$=4$\sqrt{5}$m/s
答:小车通过A点时的速度为4$\sqrt{5}$m/s.
点评 对于圆周运动动力学问题,关键要正确分析受力情况,确定向心力的来源.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
8.由上海飞往美国洛杉矶的飞机与洛杉矶飞往上海的飞机,若往返飞行时间相,且飞经太平洋上空等高匀速飞行,飞行中两种情况相比较,飞机上的乘客对座椅的压力( )
| A. | 飞机做的是匀速直线运动 | |
| B. | 飞机上的乘客对座椅的压力略大于地球对乘客的引力 | |
| C. | 飞机上的乘客对座椅的压力略小于地球对乘客的引力 | |
| D. | 飞机上的乘客对座椅的压力为零 |
6.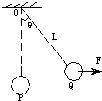 一质量为m的小球,用长为l的轻绳悬挂在O点,小球在水平拉力F作用下,从平衡位置P点缓慢地移到Q点,如图所示,则力F所做的功为( )
一质量为m的小球,用长为l的轻绳悬挂在O点,小球在水平拉力F作用下,从平衡位置P点缓慢地移到Q点,如图所示,则力F所做的功为( )
 一质量为m的小球,用长为l的轻绳悬挂在O点,小球在水平拉力F作用下,从平衡位置P点缓慢地移到Q点,如图所示,则力F所做的功为( )
一质量为m的小球,用长为l的轻绳悬挂在O点,小球在水平拉力F作用下,从平衡位置P点缓慢地移到Q点,如图所示,则力F所做的功为( )| A. | mglcosθ | B. | mgl(1-cosθ) | C. | Flcosθ | D. | Flθ |
3.关于激光的应用问题,下列说法中正确的是( )
| A. | 光纤通信是应用激光相干性的特点对信号进行调制,使其在光导纤维中传递信息的 | |
| B. | 计算机内的“激光头”读出光盘上记录的信息是应用了激光平行度好的特点 | |
| C. | 医学上可用激光做“光刀”切除肿瘤是应用激光亮度高的特点 | |
| D. | “激光测距雷达”利用激光测量很远目标的距离是应用了激光平行度好的特点 |
4.关于万有引力表达式F=$\frac{GMm}{r}$的说法正确的是( )
| A. | 表达式中G是引力常量是由卡文迪许推导并人为规定的 | |
| B. | 当r趋于0时两物体间的万有引力趋于无穷大 | |
| C. | M、m所受万有引力大小相等时是一对相互作用力 | |
| D. | 质量大的物体所受万有引力比质量小的大 |
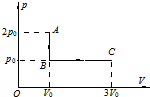 图为一定质量理想气体的压强P与体积V的关系图象,它由状态A经等容过程到状态B,再经过等压过程到状态C.设A、B、C状态对应的温度分别为TA、TB、TC,则TA=$\frac{2}{3}$TC,从状态B到状态C过程气体吸热(填“吸”、“放”)
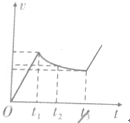
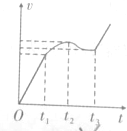
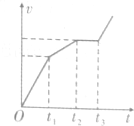
图为一定质量理想气体的压强P与体积V的关系图象,它由状态A经等容过程到状态B,再经过等压过程到状态C.设A、B、C状态对应的温度分别为TA、TB、TC,则TA=$\frac{2}{3}$TC,从状态B到状态C过程气体吸热(填“吸”、“放”)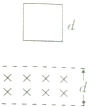 如图,竖直平面(纸面)两水平线间存在宽度为d的匀强磁场,磁场方向垂直纸面向里.一质量为m、边长也为d的正方形线圈从磁场上方某处自由落下,t1时刻线圈的下边进入磁场,t2时刻线圈的上边进入磁场,t3时刻线圈上边离开磁场.已知线圈平面在下落过程中始终与磁场方向垂直,且线圈上、下边始终与磁场边界平行,不计空气阻力,则线圈下落过程中的v-t图象可能正确的是( )
如图,竖直平面(纸面)两水平线间存在宽度为d的匀强磁场,磁场方向垂直纸面向里.一质量为m、边长也为d的正方形线圈从磁场上方某处自由落下,t1时刻线圈的下边进入磁场,t2时刻线圈的上边进入磁场,t3时刻线圈上边离开磁场.已知线圈平面在下落过程中始终与磁场方向垂直,且线圈上、下边始终与磁场边界平行,不计空气阻力,则线圈下落过程中的v-t图象可能正确的是( )
 如图所示,在溜冰场上经常看到,两人面对面拉着做圆周运动的表演,假设某光滑的溜冰场上,有甲、乙两名溜冰爱好者,M甲=80kg,M乙=40kg,面对面拉着水平的弹簧测力计做圆周运动的溜冰表演,两人相距0.9m,弹簧秤的示数为96N.求
如图所示,在溜冰场上经常看到,两人面对面拉着做圆周运动的表演,假设某光滑的溜冰场上,有甲、乙两名溜冰爱好者,M甲=80kg,M乙=40kg,面对面拉着水平的弹簧测力计做圆周运动的溜冰表演,两人相距0.9m,弹簧秤的示数为96N.求