题目内容
19.一起重机的钢绳由静止开始匀加速提起质量为m的重物,当重物的速度为v1时,起重机达到额定功率P.以后起重机保持该功率不变,继续提升重物,直到达到最大速度v2为止,则整个过程中,下列说法正确的是(重力加速度为g)( )| A. | 钢绳的最大拉力为mg | B. | 钢绳的最大拉力为$\frac{P}{{v}_{2}}$ | ||
| C. | 重物的平均速度大小为$\frac{{v}_{1}+{v}_{2}}{2}$ | D. | 重物匀加速运动的加速度$\frac{P}{m{v}_{1}}$-g |
分析 匀加速提升重物时钢绳拉力最大,且等于匀加速结束时的拉力,由P=Fv求出最大拉力;重物以最大速度为v2匀速上升时,F=mg,所以v2=$\frac{P}{F}$求出最大速度;根据牛顿第二定律求出加速度.
解答 解:A、重物匀速运动时钢绳的拉力等于重力mg,重物加速运动时处于超重状态,钢绳的拉力大于重力mg,因此钢绳的最大拉力大于mg,故A错误;
B、由P=Fv可知,钢绳匀速运动时的拉力为$\frac{P}{{v}_{2}}$,此时拉力等于重力,即$\frac{P}{{v}_{2}}$=mg,重物加速上升过程处于超重状态,钢绳的拉力大于mg,因此最大拉力大于$\frac{P}{{v}_{2}}$,故B错误;
C、重物先做匀加速直线运动,后做加速度减小的加速运动,最后做匀速直线运动,整个过程的平均速度不是$\frac{{v}_{1}+{v}_{2}}{2}$,故C错误;
D、重物匀加速运动的末速度为v1,此时的拉力为F=$\frac{P}{{v}_{1}}$,由牛顿第二定律得;a=$\frac{F-mg}{m}$=$\frac{P}{m{v}_{1}}$-g,故D正确;
故选:D.
点评 本题考查的是类似汽车的启动方式,对于汽车的两种启动方式,恒定加速度启动和恒定功率启动,对于每种启动方式的汽车运动的过程一定要熟悉.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
9.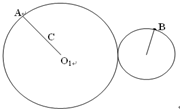 图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
 图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )| A. | A、B两点的角速度大小跟半径成反比 | |
| B. | A、B两点的角速度大小跟半径成正比 | |
| C. | A、C两点的线速度大小跟半径成反比 | |
| D. | A、C两点的线速度大小跟半径成正比 |
14.下列说法中正确的是( )
| A. | 卡文迪许发现了万有引力定律 | |
| B. | 库仑首先提出了电场的概念 | |
| C. | 牛顿首先提出了力是使物体运动的原因 | |
| D. | 元电荷e的数值最早是由美国物理学家密立根测得的 |
4. “电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )
“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )
 “电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )
“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )| A. | A球面电势比B球面电势低 | |
| B. | 电子在AB间偏转电场中做匀变速运动 | |
| C. | 等势面C所在处电场强度的大小为E=$\frac{{4{E_{k0}}}}{{e({{R_A}+{R_B}})}}$ | |
| D. | 等势面C所在处电势大小为$\frac{{{φ_A}+{φ_B}}}{2}$ |
11. 如图所示,一个长为L,质量为M的长方形木板,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度v0,从木板的左端滑向另一端,设物块与木板间的动摩擦因数为μ,当物块与木板达到相对静止时,物块仍在长木板上,物块相对木板的位移为d,木板相对地面的位移为s.则在此过程中( )
如图所示,一个长为L,质量为M的长方形木板,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度v0,从木板的左端滑向另一端,设物块与木板间的动摩擦因数为μ,当物块与木板达到相对静止时,物块仍在长木板上,物块相对木板的位移为d,木板相对地面的位移为s.则在此过程中( )
 如图所示,一个长为L,质量为M的长方形木板,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度v0,从木板的左端滑向另一端,设物块与木板间的动摩擦因数为μ,当物块与木板达到相对静止时,物块仍在长木板上,物块相对木板的位移为d,木板相对地面的位移为s.则在此过程中( )
如图所示,一个长为L,质量为M的长方形木板,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度v0,从木板的左端滑向另一端,设物块与木板间的动摩擦因数为μ,当物块与木板达到相对静止时,物块仍在长木板上,物块相对木板的位移为d,木板相对地面的位移为s.则在此过程中( )| A. | 摩擦力对物块做功为-μmg(s+d) | |
| B. | 摩擦力对木板做功为-μmgs | |
| C. | 木板动能的增量为 μmgs | |
| D. | 系统由于摩擦而产生的热量为 μmgd |
8. 如图所示,坐标原点处有一波源,起振方向为y轴负方向,形成的一列简谐横波沿x轴正方向传播.从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成如图所示的波形,此时x=4m的M点正好在波谷.下列说法中正确的是( )
如图所示,坐标原点处有一波源,起振方向为y轴负方向,形成的一列简谐横波沿x轴正方向传播.从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成如图所示的波形,此时x=4m的M点正好在波谷.下列说法中正确的是( )
 如图所示,坐标原点处有一波源,起振方向为y轴负方向,形成的一列简谐横波沿x轴正方向传播.从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成如图所示的波形,此时x=4m的M点正好在波谷.下列说法中正确的是( )
如图所示,坐标原点处有一波源,起振方向为y轴负方向,形成的一列简谐横波沿x轴正方向传播.从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成如图所示的波形,此时x=4m的M点正好在波谷.下列说法中正确的是( )| A. | P点的振动周期为0.4s | B. | P点开始振动的方向沿y轴正方向 | ||
| C. | 当M点开始振动时,P点正好在波谷 | D. | 这列波的传播速度是10m/s |




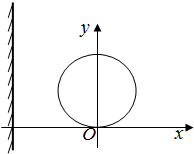 如图所示,x轴正方向水平向右,y轴正方向竖直向上.在xoy平面内有与y轴平行的匀强电场,在圆心为C半径为R的圆内还有与xoy平面垂直的匀强磁场.在原点O放置一带电微粒发射装置,它发射出质量为m、电荷量为q(q>0)和初速度大小为v的同种带电微粒,速度方向分布在xoy平面第一和第二象限内的各个方向上.已知从O点沿y轴正方向发射的带电微粒射出磁场区域后平行于x轴运动.在x轴上有一与y轴平行的荧光屏.重力加速度为g.
如图所示,x轴正方向水平向右,y轴正方向竖直向上.在xoy平面内有与y轴平行的匀强电场,在圆心为C半径为R的圆内还有与xoy平面垂直的匀强磁场.在原点O放置一带电微粒发射装置,它发射出质量为m、电荷量为q(q>0)和初速度大小为v的同种带电微粒,速度方向分布在xoy平面第一和第二象限内的各个方向上.已知从O点沿y轴正方向发射的带电微粒射出磁场区域后平行于x轴运动.在x轴上有一与y轴平行的荧光屏.重力加速度为g. 如图,一物体m在平行斜面的恒力F作用下,由静止从底端沿光滑的固定的斜面向上做匀加速直线运动,经时间t力F做功为40J,此后撤去恒力F,物体又经t时间回到出发点.求:从开始撤去力F时,物体重力势能增加了多少?
如图,一物体m在平行斜面的恒力F作用下,由静止从底端沿光滑的固定的斜面向上做匀加速直线运动,经时间t力F做功为40J,此后撤去恒力F,物体又经t时间回到出发点.求:从开始撤去力F时,物体重力势能增加了多少?