题目内容
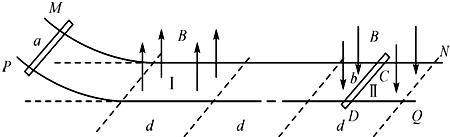
如图所示,两根间距为L的金属导轨MN和PQ,电阻不计,左端弯曲部分光滑,水平部分导轨与导体棒间的滑动摩擦因数为μ,水平导轨左端有宽度为d、方向竖直向上的匀强磁场Ⅰ,右端有另一磁场Ⅱ,其宽度也为d,但方向竖直向下,两磁场的磁感应强度大小均为B0,相隔的距离也为d。有两根质量为m、电阻均为R的金属棒a和b与导轨垂直放置,b棒置于磁场Ⅱ中点C、D处.现将a棒从弯曲导轨上某一高处由静止释放并沿导轨运动下去。
(1)当a棒在磁场Ⅰ中运动时,若要使b棒在导轨上保持静止,则a棒刚释放时的高度应小于某一值h0,求h0的大小;
(2)若将a棒从弯曲导轨上高度为h(h<h0)处由静止释放,a棒恰好能运动到磁场Ⅱ的左边界处停止,求a棒克服安培力所做的功及a棒穿过磁场Ⅰ所用的时间;
(3)若将a棒仍从弯曲导轨上高度为h(h<h0)处由静止释放,为使a棒通过磁场Ⅰ时恰好无感应电流,可让磁场Ⅱ的磁感应强度随时间而变化,将a棒刚进入磁场Ⅰ的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0,试求出在a棒通过磁场Ⅰ的这段时间里,磁场Ⅱ的磁感应强度随时间变化的关系式。

解:(1) 因为a棒进入磁场Ⅰ后做减速运动,所以只要刚进入时b棒不动,b就可以静止不动
对a棒:由机械能守恒:mgh0=![]() mv
mv![]() 对回路:ε=BLv0,I=
对回路:ε=BLv0,I=![]()
对b棒:BIL=μmg 联立解得:h0=![]() .
.
(2) 由全过程能量守恒与转化规律:mgh=μmg2d+W克A
解得:W克A=mgh-μmg2d
![]()
(3) a棒通过磁场Ⅰ时恰好无感应电流,说明感应电动势为零,
根据法拉第电磁感应定律ε=![]() ,在Δt≠0的前提下,ΔΦ=0即Φ保持不变(1分)
,在Δt≠0的前提下,ΔΦ=0即Φ保持不变(1分)
对a棒:由机械能守恒:mgh=![]() mv2
mv2
a棒进入磁场Ⅰ后,由牛顿第二定律得:a=μg
经过时间t,a棒进入磁场Ⅰ的距离为x=vt-![]() at2
at2
磁通量Φ=B0(d-x)L-B![]() L 又最初磁通量为Φ0=B0dL-B0
L 又最初磁通量为Φ0=B0dL-B0![]() L=
L=![]() B0dL=Φ
B0dL=Φ
联立解得:B=B0-![]()
![]()
*或者用微积分处理因为:ε感=ε动,ε感=![]() ·
·![]() ,ε动=B0L(v-μgt)
,ε动=B0L(v-μgt)
所以得:BB0∫dB·![]() =t0∫B0L(v-μgt)dt
=t0∫B0L(v-μgt)dt
解得(B-B0)![]() =B0L
=B0L![]() 化简得:B=B0-
化简得:B=B0-![]()
![]()

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案 如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆能刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )
如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆能刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( ) 如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆ab刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )
如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆ab刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )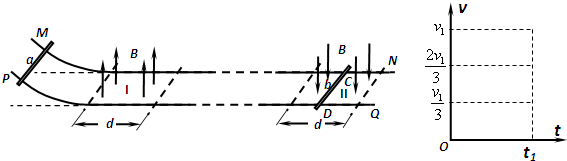
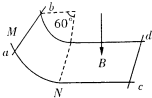 如图所示,两根间距为l的光滑金属导轨(不计电阻),由一段圆弧部分与一段无限长的水平段部分组成.其水平段加有方向竖直向下的匀强磁场,其磁感应强度为B,导轨水平段上静止放置一金属棒cd,质量为2m,电阻为2r.另一质量为m,电阻为r的金属棒ab,从圆弧段M处由静止释放下滑至N处进入水平段,圆弧段MN半径为R,所对圆心角为60°,求:
如图所示,两根间距为l的光滑金属导轨(不计电阻),由一段圆弧部分与一段无限长的水平段部分组成.其水平段加有方向竖直向下的匀强磁场,其磁感应强度为B,导轨水平段上静止放置一金属棒cd,质量为2m,电阻为2r.另一质量为m,电阻为r的金属棒ab,从圆弧段M处由静止释放下滑至N处进入水平段,圆弧段MN半径为R,所对圆心角为60°,求: