题目内容
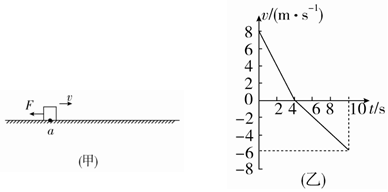
16.如图甲所示,一个可视为质点的物块从斜面底端A点滑上斜面,滑到B点时速度为零,之后又沿斜面下滑,物块运动的v-t图象如图乙所示.已知斜面倾角θ=370,物块滑上斜面的初速度为v0=40m/s,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,试求:
(1)物块在斜面上运动的最大高度;
(2)物块回到A点时的速度大小及物块从B点回到A点所用的时间.
分析 (1)根据图示图象求出物体的位移,然后求出物体上升的最大高度.
(2)由图示v-t图象求出加速度,然后应用牛顿第二定律、匀变速直线运动的速度位移公式与速度公式可以求出运动时间.
解答 解:(1)由v-t图象可知,AB间的距离:s=$\frac{1}{2}$×40×4=80m,
物块在斜面上运动的最大高度:h=ssin37°=80×0.6=48m;
(2)由v-t所示图象可知,加速度:a1=$\frac{△v}{△t}$=$\frac{40}{4}$=10m/s2,
对物块,由牛顿第二定律得:
mgsinθ+μmgcosθ=ma1,mgsinθ-μmgcosθ=ma2,
由匀变速直线运动的速度位移公式得:v2=2a2s,
解得:μ=0.5,a2=2m/s2,v=8$\sqrt{5}$m/s,
从B返回A所用时间:t=$\frac{v}{{a}_{2}}$=$\frac{8\sqrt{5}}{2}$=4$\sqrt{5}$s;
答:(1)物块在斜面上运动的最大高度为48m;
(2)物块回到A点时的速度大小及物块从B点回到A点所用的时间为4$\sqrt{5}$s.
点评 本题考查了求高度与运动时间问题,分析清楚物体的运动过程、根据图示图象求出加速度与物体的位移是解题的关键,应用牛顿第二定律与运动学公式可以解题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
6.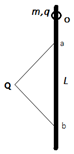 如图所示,L为竖直固定的光滑绝缘杆,杆上O点套有一质量为m、电荷量为q的带正电小环,在杆的左侧固定一电荷量为Q的正点电荷,杆上ab两点到点电荷的距离相等,现小环从图示位置的O点由静止释放,则下列说法正确的是( )
如图所示,L为竖直固定的光滑绝缘杆,杆上O点套有一质量为m、电荷量为q的带正电小环,在杆的左侧固定一电荷量为Q的正点电荷,杆上ab两点到点电荷的距离相等,现小环从图示位置的O点由静止释放,则下列说法正确的是( )
 如图所示,L为竖直固定的光滑绝缘杆,杆上O点套有一质量为m、电荷量为q的带正电小环,在杆的左侧固定一电荷量为Q的正点电荷,杆上ab两点到点电荷的距离相等,现小环从图示位置的O点由静止释放,则下列说法正确的是( )
如图所示,L为竖直固定的光滑绝缘杆,杆上O点套有一质量为m、电荷量为q的带正电小环,在杆的左侧固定一电荷量为Q的正点电荷,杆上ab两点到点电荷的距离相等,现小环从图示位置的O点由静止释放,则下列说法正确的是( )| A. | 小环从O点到b点的运动过程中可能存在受力平衡点 | |
| B. | 小环从O点到b点的运动过程,电场力做的功可能为零 | |
| C. | 小环在O、a点之间的速度一定先增大后减小 | |
| D. | 小环在O、b点之间的速度一定先减小后增加 |
4.2016年10月17日7时30分,搭载两名航天员的“神舟十一号”载人飞船由“长征二号”运载火箭成功发射升空,10月19日凌晨,“神舟十一号”飞船与“天宫二号”自动交会对接成功.“神舟十号”与“天宫一号”对接时,轨道高度是343公里,而“神舟十一号”和“天宫二号”对接时的轨道高度是393公里,这与未来空间站的轨道高度基本相同.根据以上信息,判断下列说法正确的是( )
| A. | “天宫一号”的动能比“天宫二号”的动能大 | |
| B. | “天宫一号”的周期比“天宫二号”的周期小 | |
| C. | “神舟十一号”飞船的环绕速度大于第一宇宙速度 | |
| D. | “神舟十一号”飞船必须在“天宫二号”的轨道上,再加速实现对接 |
11.一辆汽车由静止开始做加速度为a1的匀加速直线运动,加速运动了时间t1后,由于接到紧急通知,又开始做加速度为a2的匀减速直线运动,经过t2时间后停下.则汽车在全程的平均速度为( )
| A. | $\frac{{{a_1}{t_1}+{a_2}{t_2}}}{4}$ | B. | $\frac{{{a_2}{t_2}}}{2}$ | ||
| C. | $\frac{{{a_1}{t_1}^2+{a_2}{t_2}^2}}{{2({{t_1}+{t_2}})}}$ | D. | $\frac{{{a_1}{t_1}+{a_2}{t_2}}}{2}$ |
1.关于自由落体运动,下列说法中正确的是( )
| A. | 它是竖直向下,v0=0、a=g的匀加速直线运动 | |
| B. | 在开始连续的三个 1s 末的速度大小之比是 1:2:3 | |
| C. | 在开始连续的三个 1s 内通过的位移之比是 1:4:9 | |
| D. | 从开始运动起下落 4.9m、9.8m、14.7m 所经历的时间之比为 1:2:3 |
8.发现电流磁效应的科学家是( )
| A. | 欧姆 | B. | 安培 | C. | 奥斯特 | D. | 特斯拉 |
5.从某一高度相隔1s先后释放两个相同的小球甲和乙,不计空气的阻力,它们在空中任一时刻( )
| A. | 甲、乙两球的距离始终保持不变,甲、乙两球的速度之差保持不变 | |
| B. | 甲、乙两球的距离越来越大,甲、乙两球的加速度之差保持不变 | |
| C. | 甲、乙两球的距离越来越大,甲、乙两球的速度之差保持不变 | |
| D. | 甲、乙两球的距离越来越小,甲、乙两球的速度之差也越来越小 |