题目内容
 如图,竖直平面内有一个
如图,竖直平面内有一个| 3 |
| 4 |
| gR |
(1)小球通过B点时的速度大小;
(2)小球通过B点时对轨道的压力大小;
(3)AC两点间的距离.
分析:(1)小球离开B点做平抛运动,根据机械能守恒定律求解小球通过B点时的速度大小;
(2)小球到达B点时,由重力和轨道的压力的合力提供向心力,根据牛顿第二定律求出小球所受的轨道的弹力,再根据牛顿第三定律得到小球通过B点时对轨道的压力大小;
(3)小球离开B点做平抛运动,高度决定时间,根据时间和B点的速度求出水平距离,即可求得AC间的距离.
(2)小球到达B点时,由重力和轨道的压力的合力提供向心力,根据牛顿第二定律求出小球所受的轨道的弹力,再根据牛顿第三定律得到小球通过B点时对轨道的压力大小;
(3)小球离开B点做平抛运动,高度决定时间,根据时间和B点的速度求出水平距离,即可求得AC间的距离.
解答:解:(1)A点到B点,由机械能守恒定律得:
-mgR=
m
-
m
由以上解得:vB=
(2)B点由牛顿第二定律得:
F+mg=
解得:F=mg
由牛顿第三定律,小球对轨道的压力大小为mg.
(3)B到C平抛运动 R=
gt2
又 x=vBt
则 xAC=2R-R=R
则AC两点间的距离为R.
答:
(1)小球通过B点时的速度大小为
;
(2)小球通过B点时对轨道的压力大小为mg;
(3)AC两点间的距离为R.
-mgR=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 A |
由以上解得:vB=
| 2gR |
(2)B点由牛顿第二定律得:
F+mg=
| mvB2 |
| R |
解得:F=mg
由牛顿第三定律,小球对轨道的压力大小为mg.
(3)B到C平抛运动 R=
| 1 |
| 2 |
又 x=vBt
则 xAC=2R-R=R
则AC两点间的距离为R.
答:
(1)小球通过B点时的速度大小为
| 2gR |
(2)小球通过B点时对轨道的压力大小为mg;
(3)AC两点间的距离为R.
点评:解决本题的关键要分析小球圆周运动的向心力来源、掌握平抛运动、牛顿运动定律进行求解.

练习册系列答案
相关题目
 如图,竖直平面内有一光滑圆弧轨道,其半径为R=0.5m,平台与轨道的最高点等高,一质量m=lkg的小球从平台边缘的A处水平射出,恰能沿圆弧轨道上B点的切线方向进入轨道内侧,轨道半径OB与竖直线的夹角为53°,已知sin53°=0.8,cos53°=0,6,g取10m/s2.试求:
如图,竖直平面内有一光滑圆弧轨道,其半径为R=0.5m,平台与轨道的最高点等高,一质量m=lkg的小球从平台边缘的A处水平射出,恰能沿圆弧轨道上B点的切线方向进入轨道内侧,轨道半径OB与竖直线的夹角为53°,已知sin53°=0.8,cos53°=0,6,g取10m/s2.试求: (1)对于一定质量的理想气体,下列说法正确的是
(1)对于一定质量的理想气体,下列说法正确的是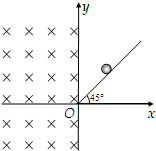 (2011?株洲二模)如图,竖直平面内有一直角坐标系xOy,在x≥0的区域内有一倾角为45°的绝缘光滑斜面,斜面末端O处用一极小的平滑曲面连接,恰能使斜面末端水平.在x≤0的广泛区域内存在正交的匀强磁场和匀强电场,磁场垂直于纸面向里,磁感应强度大小为B;电场沿竖直方向,场强大小为E.电荷量为-q的带电小球从绝缘光滑斜面上某点由静止开始下滑,小球经斜面末端O点进入电场和磁场,之后沿圆周运动,垂直于y轴离开电场和磁场,最后垂直打到斜面上.
(2011?株洲二模)如图,竖直平面内有一直角坐标系xOy,在x≥0的区域内有一倾角为45°的绝缘光滑斜面,斜面末端O处用一极小的平滑曲面连接,恰能使斜面末端水平.在x≤0的广泛区域内存在正交的匀强磁场和匀强电场,磁场垂直于纸面向里,磁感应强度大小为B;电场沿竖直方向,场强大小为E.电荷量为-q的带电小球从绝缘光滑斜面上某点由静止开始下滑,小球经斜面末端O点进入电场和磁场,之后沿圆周运动,垂直于y轴离开电场和磁场,最后垂直打到斜面上. 如图,竖直平面内有一直角形内径相同的 细玻璃管,A端封闭,C端开口,AB=BC=l0,且此时A、C端等高.管内水银总长度为l0,玻璃管AB内封闭有长为
如图,竖直平面内有一直角形内径相同的 细玻璃管,A端封闭,C端开口,AB=BC=l0,且此时A、C端等高.管内水银总长度为l0,玻璃管AB内封闭有长为 ,且此时A、C端等高。平街时,管内水银总长度为
,且此时A、C端等高。平街时,管内水银总长度为