题目内容
19.质量为0.05kg的子弹以600m/s的速度水平射入静止的木块,木块的质量为2.95kg,放在光滑的水平桌面上.子弹和木块最终的速度为10m/s;损失的动能全部转化为内能,求:①子弹损失的动能;
②木块和子弹共同增加的内能.
分析 (1)以子弹与木块组成的系统为研究对象,由动量守恒定律可以求出子弹和木块的共同速度,由△Ek=$\frac{1}{2}$mv2-$\frac{1}{2}$mv${\;}_{0}^{2}$求出子弹损失的动能
(2)应用能量守恒求木块和子弹共同增加的内能
解答 解:(1)以子弹与木块组成的系统为研究对象,以子弹的初速度方向为正方向,由动量守恒定律得:
mv0=(m+M)v,
代入数据解得:v=10m/s;
由△Ek=$\frac{1}{2}$mv2-$\frac{1}{2}$mv${\;}_{0}^{2}$得子弹损失的动能为:
△Ek=8997.5J
(2)由能量守恒得木块和子弹共同增加的内能为:
△E=$\frac{1}{2}$mv${\;}_{0}^{2}$-$\frac{1}{2}$(m+M)v2=$\frac{1}{2}×$0.05×6002-$\frac{1}{2}×$(0.05+2.95)×102=8850J
答:①子弹损失的动能8997.5J
②木块和子弹共同增加的内能8850J.
点评 子弹穿过木块的过程,子弹与木块组成的相同动量守恒,由动量守恒定律与动能定理可以正确解题,解题时注意研究对象、研究过程的选择.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 如图所示,A、B两个质量相同的小球,用细线相连,一轻质弹簧的上端固定于O点,下端与A球相连接,两球处于静止状态.现将细线烧断,则在烧断的瞬间两球的加速度是( )
如图所示,A、B两个质量相同的小球,用细线相连,一轻质弹簧的上端固定于O点,下端与A球相连接,两球处于静止状态.现将细线烧断,则在烧断的瞬间两球的加速度是( )
 如图所示,A、B两个质量相同的小球,用细线相连,一轻质弹簧的上端固定于O点,下端与A球相连接,两球处于静止状态.现将细线烧断,则在烧断的瞬间两球的加速度是( )
如图所示,A、B两个质量相同的小球,用细线相连,一轻质弹簧的上端固定于O点,下端与A球相连接,两球处于静止状态.现将细线烧断,则在烧断的瞬间两球的加速度是( )| A. | A、B两球的加速度大小都等于g,但方向相反 | |
| B. | A球的加速度为2g,方向向上,B球的加速度为g,方向向下 | |
| C. | A球的加速度为g,方向向上,B球的加速度为零 | |
| D. | A球的加速度为零,B球的加速度为g,方向向下 |
4. 穿在光滑曲杆上的质量为m的小球从A点以初速度v0释放,沿曲杆运动最终落地,B点离地高度为h1,C点离地高度为h2,(h1>h2),为使得小环落地动能最小,则在A处重力势能为(以地面为零势能面,重力加速度为g)( )
穿在光滑曲杆上的质量为m的小球从A点以初速度v0释放,沿曲杆运动最终落地,B点离地高度为h1,C点离地高度为h2,(h1>h2),为使得小环落地动能最小,则在A处重力势能为(以地面为零势能面,重力加速度为g)( )
 穿在光滑曲杆上的质量为m的小球从A点以初速度v0释放,沿曲杆运动最终落地,B点离地高度为h1,C点离地高度为h2,(h1>h2),为使得小环落地动能最小,则在A处重力势能为(以地面为零势能面,重力加速度为g)( )
穿在光滑曲杆上的质量为m的小球从A点以初速度v0释放,沿曲杆运动最终落地,B点离地高度为h1,C点离地高度为h2,(h1>h2),为使得小环落地动能最小,则在A处重力势能为(以地面为零势能面,重力加速度为g)( )| A. | mgh1 | B. | mgh2 | C. | mgh1-$\frac{1}{2}$mv02 | D. | mgh2-$\frac{1}{2}$mv02 |
10.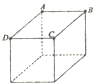 在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
 在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )
在边长为20cm的正方体顶点A、B、C上分别放置3个完全相同的点电荷,电荷量均为+4×10-6C,静电力常量K=9.0×109N•m2/C2.则A、C两点电荷对B点电荷的作用力为( )| A. | $\sqrt{2}$N | B. | 2$\sqrt{2}$N | C. | 3.6$\sqrt{2}$N | D. | 3.6$\sqrt{3}$N |
 如图所示,abcde是半径为r的圆内接正五边形,在其顶点a、b、c、d处各固定电荷量为+Q的点电荷,在e处固定电荷量为-3Q的点电荷,则放置在圆心O处的电荷量为-q的点电荷所受到的静电力的大小为$\frac{4kQ}{{r}^{2}}$,方向为沿Oe方向.
如图所示,abcde是半径为r的圆内接正五边形,在其顶点a、b、c、d处各固定电荷量为+Q的点电荷,在e处固定电荷量为-3Q的点电荷,则放置在圆心O处的电荷量为-q的点电荷所受到的静电力的大小为$\frac{4kQ}{{r}^{2}}$,方向为沿Oe方向.







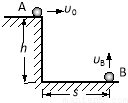 如图所示,在高为h的平台边缘水平抛出小球A,同时在水平地面上距台面边缘水平距离为s处竖直上抛小球B,两球运动轨迹在同一竖直平面内,不计空气阻力,重力加速度为g.若两球能在空中相遇,则小球A的初速度v0应大于$s\sqrt{\frac{g}{2h}}$,A、B两球初速度之比$\frac{{v}_{0}}{{v}_{B}}$为$\frac{s}{h}$.
如图所示,在高为h的平台边缘水平抛出小球A,同时在水平地面上距台面边缘水平距离为s处竖直上抛小球B,两球运动轨迹在同一竖直平面内,不计空气阻力,重力加速度为g.若两球能在空中相遇,则小球A的初速度v0应大于$s\sqrt{\frac{g}{2h}}$,A、B两球初速度之比$\frac{{v}_{0}}{{v}_{B}}$为$\frac{s}{h}$.