题目内容
9. 在光滑水平面上静置有质量均为m的木板AB和滑块CD,木板AB上表面粗糙,滑块CD上表面是光滑的$\frac{1}{4}$圆弧,其始端D点切线水平且在木板AB上表面内,它们紧靠在一起,如图所示.一可视为质点的物块P,质量也为m,从木板AB的右端以初速度v0滑上木板AB,过B点时速度为$\frac{{v}_{0}}{2}$,又滑上滑块CD,最终恰好能滑到滑块CD圆弧的最高点C处,求:
在光滑水平面上静置有质量均为m的木板AB和滑块CD,木板AB上表面粗糙,滑块CD上表面是光滑的$\frac{1}{4}$圆弧,其始端D点切线水平且在木板AB上表面内,它们紧靠在一起,如图所示.一可视为质点的物块P,质量也为m,从木板AB的右端以初速度v0滑上木板AB,过B点时速度为$\frac{{v}_{0}}{2}$,又滑上滑块CD,最终恰好能滑到滑块CD圆弧的最高点C处,求:(1)物块滑到B处时木板的速度VAB;
(2)滑块CD圆弧的半径R.
分析 对系统运用动量守恒定律,根据动量守恒定律求出物块滑到B处时木板的速度.
物块恰好能滑到圆弧的最高点C处,知物块与圆弧轨道具有相同的速度,根据动量守恒定律和机械能守恒定律求出圆弧的半径.
解答 解:(1)由点A到点B过程中.在水平方向上合外力为零,动量守恒,取向左为正.有:
mv0=mvB+2m•vAB ,
又vB=$\frac{{v}_{0}}{2}$,
解得:vAB=$\frac{{v}_{0}}{4}$
(2)由点D到点C,滑块CD与物块P水平方向动量守恒,
m$•\frac{1}{2}$v0+m$•\frac{1}{4}$v0=2m•v共,
根据机械能守恒得:
mgR=$\frac{1}{2}$$m(\frac{{v}_{0}}{4})^{2}$+$\frac{1}{2}m(\frac{{v}_{0}}{2})^{2}$-$\frac{1}{2}$×2m(v共)2
解之得:v共=$\frac{{3v}_{0}}{8}$,R=$\frac{{{v}_{0}}^{2}}{64g}$
答:(1)物块滑到B处时木板的速度为$\frac{{v}_{0}}{4}$;
(2)滑块CD圆弧的半径为$\frac{{{v}_{0}}^{2}}{64g}$.
点评 解决该题关键要能够熟练运用动量守恒定律和机械能守恒定律列出等式求解,注意题目中的条件,物块恰好能滑到圆弧的最高点C处,则物块与圆弧轨道具有相同的速度,难度适中.

练习册系列答案
相关题目
19.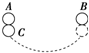 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )| A. | $\frac{F}{8}$ | B. | $\frac{F}{4}$ | C. | $\frac{3F}{8}$ | D. | $\frac{3F}{4}$ |
20.如图,一平面简谐波以波速u沿x轴正方形传播,O为坐标原点,已知P点的振动方程为y=Acosωt,则( )
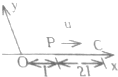

| A. | O点的振动方程为y=Acosω(t-$\frac{1}{u}$) | B. | 波的表达式为y=Acosω[t-($\frac{1}{u}$)-($\frac{x}{u}$)] | ||
| C. | 波的表达式为y=Acosω[t+($\frac{1}{u}$)-($\frac{x}{u}$)] | D. | C点的振动方程为y=Acosω(t-$\frac{3l}{u}$) |
4. 如图所示,两块相对的平行金属板M、N与电池相连,N板接地.在距离两板等远的一点P固定一个带负电的点电荷,如果将M板向上移一小段距离,则( )
如图所示,两块相对的平行金属板M、N与电池相连,N板接地.在距离两板等远的一点P固定一个带负电的点电荷,如果将M板向上移一小段距离,则( )
 如图所示,两块相对的平行金属板M、N与电池相连,N板接地.在距离两板等远的一点P固定一个带负电的点电荷,如果将M板向上移一小段距离,则( )
如图所示,两块相对的平行金属板M、N与电池相连,N板接地.在距离两板等远的一点P固定一个带负电的点电荷,如果将M板向上移一小段距离,则( )| A. | 点电荷将向下运动 | B. | P点的电势升高 | ||
| C. | 点电荷的电势能增大 | D. | 极板带电量增大 |
14. 如图所示的塔吊,正在将质量为50kg的建筑材料从地面开始以加速度a=0.5m/s2吊起,经过4s后,则(重力加速度g=10m/s2)( )
如图所示的塔吊,正在将质量为50kg的建筑材料从地面开始以加速度a=0.5m/s2吊起,经过4s后,则(重力加速度g=10m/s2)( )
 如图所示的塔吊,正在将质量为50kg的建筑材料从地面开始以加速度a=0.5m/s2吊起,经过4s后,则(重力加速度g=10m/s2)( )
如图所示的塔吊,正在将质量为50kg的建筑材料从地面开始以加速度a=0.5m/s2吊起,经过4s后,则(重力加速度g=10m/s2)( )| A. | 物体的动能为2100J | B. | 钢绳的拉力对物体做功2000J | ||
| C. | 物体的重力势能增加了100J | D. | 物体的机械能增加了2100J |
1. 同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )
同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )
 同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )
同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )| A. | 开动B的小发动机向前喷气,使B适当减速,可使卫星回到同步轨道 | |
| B. | B的速率大于C的速率 | |
| C. | 开动C的小发动机向前喷气,使C适当减速,可使卫星回到同步轨道 | |
| D. | B的角速度大于C的角速度 |
