题目内容
19. 如图所示是小明自制的简易温度计.在空玻璃瓶内插入一根两端开口、内横截面积为0.4cm2的玻璃管,玻璃瓶与玻璃管接口处用蜡密封,整个装置水平放置.玻璃管内有一段长度可忽略不计的水银柱,当大气压为1.0×105P,气温为7℃时,水银柱刚好位于瓶口位置,此时封闭气体体积为480cm3,瓶口外玻璃管有效长度为48cm.求:
如图所示是小明自制的简易温度计.在空玻璃瓶内插入一根两端开口、内横截面积为0.4cm2的玻璃管,玻璃瓶与玻璃管接口处用蜡密封,整个装置水平放置.玻璃管内有一段长度可忽略不计的水银柱,当大气压为1.0×105P,气温为7℃时,水银柱刚好位于瓶口位置,此时封闭气体体积为480cm3,瓶口外玻璃管有效长度为48cm.求:①此温度计能测量的最高气温;
②当气温从7℃缓慢上升到最高气温的过程中,密封气体吸收的热量为3J,则在这一过程中密封气体的内能变化了多少.
分析 ①气体发生等压变化,根据盖吕萨克定律直接求解
②根据热力学第一定律列式求解
解答 解:①当水银柱到达管口时,达到能测量的最高气温${T}_{2}^{\;}$,则
初状态:${T}_{1}^{\;}=(273+7)K=280K$ ${V}_{1}^{\;}=480c{m}_{\;}^{3}$
末状态:${V}_{2}^{\;}=(480+48×0.4)c{m}_{\;}^{3}=499.2c{m}_{\;}^{3}$
由盖吕萨克定律得$\frac{{V}_{1}^{\;}}{{T}_{1}^{\;}}=\frac{{V}_{2}^{\;}}{{T}_{2}^{\;}}$
代入数据得:${T}_{2}^{\;}=291.2K$,
即:${t}_{2}^{\;}=18.2℃$
②水银移动到管右端的过程中,外界对气体做功为:
$W=-{p}_{0}^{\;}SL=-1.92J$
由热力学第一定律得气体内能变化为:
△U=W+Q=-1.92+3=1.08J
答:①此温度计能测量的最高气温18.2℃;
②在这一过程中密封气体的内能增加了1.08J.
点评 本题考查了求温度、内能的变化量,分析清楚气体状态变化过程,应用盖吕萨克定律、热力学第一定律即可解题.

练习册系列答案
相关题目
11.下列叙述正确的是( )
| A. | 用热针尖接触金属表面的石蜡,融化区域呈圆形,说明金属是非晶体 | |
| B. | 扩散现象和布朗运动的剧烈程度都与温度有关,所以扩散现象和布朗运动也叫作热运动 | |
| C. | 空气相对湿度越大时,空气中压强越接近饱和气压,水蒸发越慢 | |
| D. | 1mol氧气和1mol氢气,(可看做理想气体)在0℃时的内能相同 | |
| E. | 晶体融化过程中,当温度达到熔点时,吸收的热量全部用来破坏空间点阵,增加分子势能,而分子平均动能却保持不变 |
12.在某行星和地球表面以相同的速率分别竖直上抛一个物体,它们各自返回抛出点的时间之比为1:2,已知该行星质量约为地球质量的4倍,地球的半径为R,由此可知,该行星的半径为( )
| A. | $\frac{1}{2}$R | B. | $\frac{\sqrt{2}}{2}$R | C. | $\sqrt{2}$R | D. | 2R |
4.质量为m的物体从高h处以$\frac{g}{3}$的加速度由静止竖直下落到地面,下列说法中正确的是( )
| A. | 物体的机械能减少$\frac{2mgh}{3}$ | B. | 物体的重力势能减少$\frac{mgh}{3}$ | ||
| C. | 物体的动能增加$\frac{mgh}{3}$ | D. | 重力做功为mgh |
8. 如图所示,导线圈与电流表组成闭合回路,当手持条形磁铁使它的一个磁极靠近线圈的一端时,以下说法正确的是( )
如图所示,导线圈与电流表组成闭合回路,当手持条形磁铁使它的一个磁极靠近线圈的一端时,以下说法正确的是( )
 如图所示,导线圈与电流表组成闭合回路,当手持条形磁铁使它的一个磁极靠近线圈的一端时,以下说法正确的是( )
如图所示,导线圈与电流表组成闭合回路,当手持条形磁铁使它的一个磁极靠近线圈的一端时,以下说法正确的是( )| A. | 线圈的上端和磁铁的上端是同名磁极 | |
| B. | 人克服磁场力做功,把其他形式的能转化为线圈的电能 | |
| C. | 从能量守恒的角度看,有外力对磁体和线圈组成的系统作了功 | |
| D. | 楞次定律是能量守恒在电磁感应现象中的具体反映 |
9.长为a、宽为b的矩形线圈,在磁感应强度为B的匀强磁场中,绕垂直于磁场的OO′轴以恒定的角速度ω旋转.设t=0时,线圈平面与磁场方向平行,则此时的磁通量的变化率和磁通量分别是( )
| A. | Babω,0 | B. | 0,Babω | C. | $\frac{Babω}{\sqrt{2}}$,0 | D. | Babω,Babω |
 如图所示,有两个不计厚度的活塞M、N将两部分理想气体A、B封闭在竖直放置的绝热气缸内,温度均为27℃.M活塞是导热的,N活塞是绝热的,均可沿气缸无摩擦地滑动,气缸底部有加热丝.已知M活塞的质量m1=1kg,N活塞的质量不计.M、N活塞的横截面积均为S=2cm2,初始时M活塞相对于底部的高度为h1=24cm,N活塞相对于底部的高度为h2=12cm.现将一质量为m2=1kg的小物体放在M活塞的上表面上,活塞下降,稳定后B气体压强为P2.已知大气压强为P0=1.0×105Pa,取g=10m/s2.
如图所示,有两个不计厚度的活塞M、N将两部分理想气体A、B封闭在竖直放置的绝热气缸内,温度均为27℃.M活塞是导热的,N活塞是绝热的,均可沿气缸无摩擦地滑动,气缸底部有加热丝.已知M活塞的质量m1=1kg,N活塞的质量不计.M、N活塞的横截面积均为S=2cm2,初始时M活塞相对于底部的高度为h1=24cm,N活塞相对于底部的高度为h2=12cm.现将一质量为m2=1kg的小物体放在M活塞的上表面上,活塞下降,稳定后B气体压强为P2.已知大气压强为P0=1.0×105Pa,取g=10m/s2.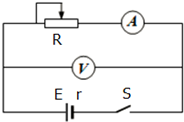 如图所示为测干电池的电动势和内阻的电路图,用两节干电池串联作为电源(每节电池电动势接近1.5V,内阻约为0.5Ω),除给出的电源、导线和开关外,还有以下器材:
如图所示为测干电池的电动势和内阻的电路图,用两节干电池串联作为电源(每节电池电动势接近1.5V,内阻约为0.5Ω),除给出的电源、导线和开关外,还有以下器材: 如图所示,倾斜放置的传送带与水平面的夹角θ=37°,在电动机的带动下保持v=2m/s的速率顺时针匀速运行.底端和上端分别有离传送带很近的挡板P、Q,它们不影响传送带的运行,但可将传送带上的物块挡住,P、Q之间距离L=15m.将物块从O点静止释放,运动一段时间后与挡板碰撞,O点距P的距离LOP=4m.已知物块与挡板碰撞时间极短,碰撞前、后速度大小不变,物块可视为质点,物块的质量为m=10kg,物块与传送带间的动摩擦因数μ=0.5,假设最大静摩擦力是滑动摩擦力的1.7倍.sin37°=0.6,cos37°=0.8,取g=10m/s2.传送带与轮子间无相对滑动,不计轮轴处的摩擦.求:
如图所示,倾斜放置的传送带与水平面的夹角θ=37°,在电动机的带动下保持v=2m/s的速率顺时针匀速运行.底端和上端分别有离传送带很近的挡板P、Q,它们不影响传送带的运行,但可将传送带上的物块挡住,P、Q之间距离L=15m.将物块从O点静止释放,运动一段时间后与挡板碰撞,O点距P的距离LOP=4m.已知物块与挡板碰撞时间极短,碰撞前、后速度大小不变,物块可视为质点,物块的质量为m=10kg,物块与传送带间的动摩擦因数μ=0.5,假设最大静摩擦力是滑动摩擦力的1.7倍.sin37°=0.6,cos37°=0.8,取g=10m/s2.传送带与轮子间无相对滑动,不计轮轴处的摩擦.求: